

Next: Perturbative cranking approximation
Up: Cranking approximation
Previous: Quasiparticle basis
The collective mass involves either derivatives of the density
matrices or the mean-field potentials. It should be stressed that
these derivatives must be calculated in the original single-particle
basis 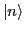 as the canonical basis (5) varies with
as the canonical basis (5) varies with
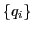 . In the following, we show how to evaluate the collective
derivatives in the one-dimensional case of single collective
coordinate, the quadrupole deformation
. In the following, we show how to evaluate the collective
derivatives in the one-dimensional case of single collective
coordinate, the quadrupole deformation 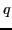 . To this end, we
approximate the derivative of the density operator
. To this end, we
approximate the derivative of the density operator 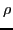 or
or 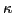 at a deformation point
at a deformation point 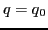 by means of the Lagrange three-point
formula for unequally spaced points
by means of the Lagrange three-point
formula for unequally spaced points 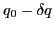 ,
, 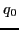 , and
, and 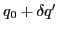 [12,9,16]:
[12,9,16]:
The reason for the use of unequally spaced grid in Eq. (52) is
purely numerical: the constrained HFB equations cannot be precisely
solved at a requested deformation point 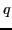 .
.
The corresponding matrix element in the canonical basis can be
expressed through the matrices 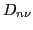 of the canonical
transformation (5):
of the canonical
transformation (5):
It should be noted that the canonical matrix 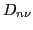 in the above
expression corresponds to the deformation point,
in the above
expression corresponds to the deformation point, 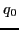 , at which the
mass is evaluated. Furthermore, as mentioned above, the density
matrices at the three deformation points in (52) need to be
calculated using the single-particle basis
, at which the
mass is evaluated. Furthermore, as mentioned above, the density
matrices at the three deformation points in (52) need to be
calculated using the single-particle basis 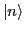 with the same basis
deformation.
with the same basis
deformation.


Next: Perturbative cranking approximation
Up: Cranking approximation
Previous: Quasiparticle basis
Jacek Dobaczewski
2010-07-28
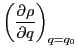
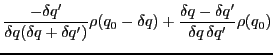
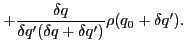
![]() of the canonical
transformation (5):
of the canonical
transformation (5):