


Next: Summary of ATDHFB
Up: ATDHFB Theory
Previous: ATDHFB Theory
We begin with the HFB approach. In what follows, we use the
same notation as in Ref. [15]. The HFB formalism can be
conveniently expressed in terms of the generalized density matrix,
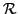 , defined as
, defined as
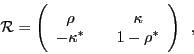 |
(1) |
where 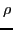 and
and 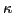 are the particle and pairing densities
and
are the particle and pairing densities
and
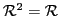 .
The energy variation results in the HFB
equation
.
The energy variation results in the HFB
equation
![\begin{displaymath}[{\cal W}, {\cal R}]=0\,\,\,,
\end{displaymath}](img16.png) |
(2) |
which can be written as a non-linear
eigenvalue problem:
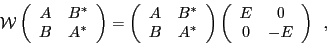 |
(3) |
where
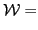 |
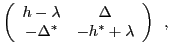 |
|
(4) |
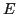 is a diagonal matrix of quasiparticle energies
is a diagonal matrix of quasiparticle energies 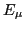 ,
,
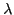 is the chemical potential,
and matrices
is the chemical potential,
and matrices 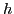 and
and 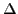 are the
particle-hole and pairing mean-field potentials [1], respectively.
are the
particle-hole and pairing mean-field potentials [1], respectively.
For the sake of comparison with the commonly used BCS formalism, it is quite useful to write the HFB equations in the canonical
representation. The single-particle canonical wave function
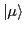 can be expanded in the original
single-particle (harmonic oscillator) basis
can be expanded in the original
single-particle (harmonic oscillator) basis 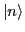 as
as
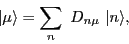 |
(5) |
where the unitary transformation 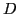 is obtained by diagonalizing the
density matrix
is obtained by diagonalizing the
density matrix 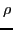 . In the canonical basis, the HFB wave function is
given in a BCS-like form:
. In the canonical basis, the HFB wave function is
given in a BCS-like form:
where the phase 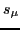 , for the time-even quasiparticle vacuum considered here, is defined through the
time-inversion of the single-particle states
, for the time-even quasiparticle vacuum considered here, is defined through the
time-inversion of the single-particle states
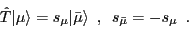 |
(8) |
In Eq. (6) and in the following, the quantities in the canonical basis are denoted by
symbols with breve accents [15].
The HFB energy matrix 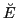 in the canonical basis is non-diagonal
and is given by
in the canonical basis is non-diagonal
and is given by
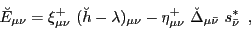 |
(9) |
where
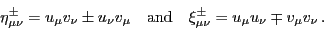 |
(10) |
The diagonal matrix elements of the matrix
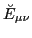 can be
written as [1,15]:
can be
written as [1,15]:
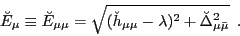 |
(11) |
Even though the above equation resembles the BCS expression for
quasiparticle energy, it involves
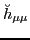 and
and
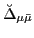 , which are respectively obtained by
transforming the HFB particle-hole and the pairing fields to the
canonical basis via the transformation (5). It is only
in the BCS approximation that these quantities can be associated with
single-particle energies and the pairing gap.
, which are respectively obtained by
transforming the HFB particle-hole and the pairing fields to the
canonical basis via the transformation (5). It is only
in the BCS approximation that these quantities can be associated with
single-particle energies and the pairing gap.



Next: Summary of ATDHFB
Up: ATDHFB Theory
Previous: ATDHFB Theory
Jacek Dobaczewski
2010-07-28
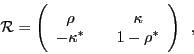
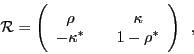
![]() can be expanded in the original
single-particle (harmonic oscillator) basis
can be expanded in the original
single-particle (harmonic oscillator) basis ![]() as
as
![]() in the canonical basis is non-diagonal
and is given by
in the canonical basis is non-diagonal
and is given by