


Next: Approximations to ATDHFB
Up: ATDHFB Theory
Previous: Summary of HFB
The ATDHFB approach is an approximation to the time-dependent HFB theory,
wherein it is assumed that the collective velocity of the system is
small compared to the average single-particle velocity of the
nucleons. The generalized HFB density matrix is expanded around the
quasi-stationary HFB solution 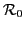 up to quadratic terms in the collective momentum:
up to quadratic terms in the collective momentum:
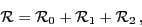 |
(12) |
with 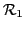 being time-odd and
being time-odd and 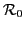 and
and 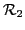 time-even densities. The
corresponding expansion for the HFB Hamiltonian reads
time-even densities. The
corresponding expansion for the HFB Hamiltonian reads
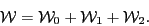 |
(13) |
Employing the density expansion (12), the HFB energy can be separated
into the collective kinetic and the potential parts. In terms of the
density expansion (12), the kinetic energy is given by
In the usual ATDHFB treatment, the second term involving 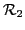 is neglected, and the kinetic energy can be written in the familiar
form:
is neglected, and the kinetic energy can be written in the familiar
form:
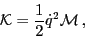 |
(15) |
where the collective mass is given by
The trace in the above expression can easily be evaluated in the
quasiparticle basis. To this end, one can utilize the ATDHFB equation
[3,4,5,6]
![\begin{displaymath}
i {\dot {\cal R}_0} = [{\cal W}_0, {\cal R}_1 ] +
[ {\cal W}_1, {\cal R}_0]\,.
\end{displaymath}](img55.png) |
(18) |
In the quasiparticle basis, the matrices
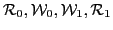 , and
, and
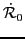 are represented by the matrices
are represented by the matrices
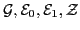 , and
, and 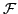 , respectively:
, respectively:
where
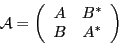 |
(24) |
is the matrix of the Bogolyubov transformation, and
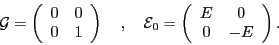 |
(25) |
ATDHFB equation (18) can now be written in the
quasiparticle basis as
![\begin{displaymath}
i {\cal F} = [{\cal E}_0, {\cal Z} ] +
[{\cal E}_1 \,, {\cal G}] \,.
\end{displaymath}](img72.png) |
(26) |
This 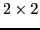 matrix equation is, in fact, equivalent [6]
to the following equation,
matrix equation is, in fact, equivalent [6]
to the following equation,
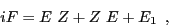 |
(27) |
where the antisymmetric matrices 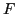 ,
, 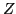 , and
, and 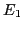 are
related to
are
related to 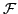 ,
, 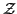 , and
, and 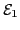 :
:
In the case of several collective coordinates 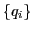 ,
the ATDHFB equation (18) must be solved for each coordinate,
,
the ATDHFB equation (18) must be solved for each coordinate,
![\begin{displaymath}
i {\dot q}_i\frac {\partial {\cal R}_0}
{\partial q_i} = [{\cal W}_0, {\cal R}_1^i ] +
[ {\cal W}_1^i, {\cal R}_0]\, ,
\end{displaymath}](img86.png) |
(30) |
and the collective mass tensor becomes:
![\begin{displaymath}
{\cal M}_{ij} = \frac {i} {2\dot q_j}
{\rm Tr} \biggr( \frac...
...\cal R}_0}
{\partial q_i} [{\cal R}_0, {\cal R}_1^j] \biggr).
\end{displaymath}](img87.png) |
(31) |
Then, in terms of the corresponding matrices 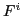 and
and 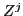 , the
collective mass tensor is given by
, the
collective mass tensor is given by
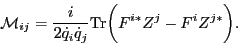 |
(32) |
The expression (32) for the mass tensor contains the matrix 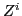 , which is
associated with time-odd density matrix
, which is
associated with time-odd density matrix 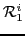 and can, in
principle, be obtained by solving the HFB equations with time-odd
fields. The time-odd fields have been incorporated in mass-tensor
calculations only in a limited number of cases. For instance, in
Ref. [12], time-odd fields have been included in the HF study
with a constraint of cylindrical symmetry. The
time-odd fields have also been incorporated in the HFB study in an
approximate iterative scheme with the collective path based on the
Woods-Saxon potential [6].
and can, in
principle, be obtained by solving the HFB equations with time-odd
fields. The time-odd fields have been incorporated in mass-tensor
calculations only in a limited number of cases. For instance, in
Ref. [12], time-odd fields have been included in the HF study
with a constraint of cylindrical symmetry. The
time-odd fields have also been incorporated in the HFB study in an
approximate iterative scheme with the collective path based on the
Woods-Saxon potential [6].



Next: Approximations to ATDHFB
Up: ATDHFB Theory
Previous: Summary of HFB
Jacek Dobaczewski
2010-07-28
![]() up to quadratic terms in the collective momentum:
up to quadratic terms in the collective momentum:
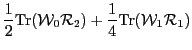
![$\displaystyle \frac {i} {4} {\rm Tr} \left( {\dot {\cal R}_0} [{ \cal R}_0,
{ \...
...c {1} {2} \left( [ {\cal R}_2, { \cal R}_0]
[{ \cal W}_0, { \cal R}_0] \right).$](img50.png)
![]() ,
the ATDHFB equation (18) must be solved for each coordinate,
,
the ATDHFB equation (18) must be solved for each coordinate,