1Institute of Theoretical Physics, Warsaw University,
Hoza 69, PL-00681, Warsaw, Poland
2Institut de Recherches Subatomiques,
UMR7500, CNRS-IN2P3 and Université Louis Pasteur,
F-67037 Strasbourg Cedex 2, France
P. Olbratowski,1,2 J. Dobaczewski,1,2 and J. Dudek2
Spontaneous chiral symmetry breaking constitutes an interesting type of collective effect in fermion systems [1]. In the present context, a system is called chiral if it is not related to its time-reversed partner by a spatial rotation. A rotating triaxial body with its angular momentum pointing towards one of the octants of the intrinsic coordinate system, where the short (s), medium (m) and long (l) axes form either a left- or right-handed set, is an example. In the laboratory frame, the chiral rotation leads to pairs of rotational bands. Rigid bodies with no internal structure cannot rotate freely in such a way, and therefore, investigation of the chiral rotation may give us information on the underlying internal properties.
Triaxiality is common in molecules where it arises from a spatial arrangement of the constituent atoms. In nuclei it can be induced by shell effects. It has been suggested [1] that appearance of chiral doublets may provide a strong evidence for nuclear triaxiality. Candidates for such doublets were recently observed in several N=75 isotones [2], 132La among them. Calculations within the particle-rotor model [3] confirm their possible chiral character.
As proposed in Ref. [4], the chiral rotation may appear if a few proton particles occupy the lowest substates of a high-jorbital, and simultaneously a few neutron holes are left in the highest substates. The former drive the nucleus towards elongated shapes, while the latter towards disc-like shapes. An interplay of these opposite tendencies may yield triaxiality. It also turns out that the considered particles and holes align their angular momenta along the short and long axes, respectively. As follows from hydrodynamical considerations [5], the moment of inertia along the medium axis is the largest, thus favoring the collective core rotation around this axis. Therefore, the total spin has non-zero components on all axes, creating the possibility of left- or right-handed rotation.
In the present study we consider the
![]() configuration in 132La,
which fulfills the above prerequisite conditions for the chiral
rotation. Our analysis is based on the Hartree-Fock (HF) cranking
calculations [6] with the angular frequency vector that can
arbitrarily orient itself with respect to the mass distribution
(Tilted-Axis Cranking (TAC) model [7]). In all HF
solutions found in 132La a stable triaxial deformation of about
configuration in 132La,
which fulfills the above prerequisite conditions for the chiral
rotation. Our analysis is based on the Hartree-Fock (HF) cranking
calculations [6] with the angular frequency vector that can
arbitrarily orient itself with respect to the mass distribution
(Tilted-Axis Cranking (TAC) model [7]). In all HF
solutions found in 132La a stable triaxial deformation of about
![]() and
and
![]() was obtained. In the framework
of the TAC model, with phenomenological mean field, chiral solutions
were already obtained in 134Pr and 188Ir [8].
was obtained. In the framework
of the TAC model, with phenomenological mean field, chiral solutions
were already obtained in 134Pr and 188Ir [8].
In order to study the rotational properties of the single-particle
(s.p.) orbitals in question, we first applied the angular-momentum
cranking in the s-l plane for
0<
![]() ,
,
![]() <0.5MeV. Calculations were
performed non-selfconsistently, starting from the converged HF
solution obtained at
<0.5MeV. Calculations were
performed non-selfconsistently, starting from the converged HF
solution obtained at
![]() =0.
=0.
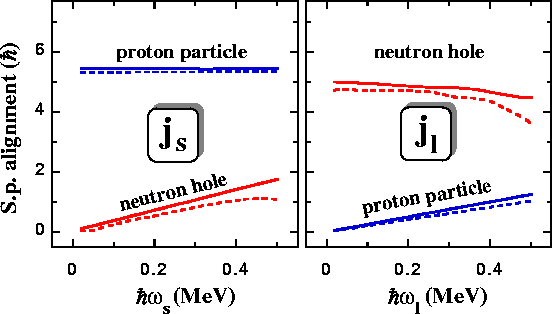 |
Note, that the above analysis could not be done self-consistently,
because we oriented vector
![]() along all directions in the
intrinsic frame. In self-consistent solutions its orientation is
constrained by the Kerman-Onishi theorem [9] requiring
that
along all directions in the
intrinsic frame. In self-consistent solutions its orientation is
constrained by the Kerman-Onishi theorem [9] requiring
that
![]() and
and
![]() be parallel.
be parallel.
To examine the collective rotational behavior we now turn to
self-consistent calculations with the standard axial cranking, that
is when both
![]() and
and
![]() point along either of the
three principal axes of the mass distribution. Figure
2 shows the properties of the three resulting bands
at frequencies of
point along either of the
three principal axes of the mass distribution. Figure
2 shows the properties of the three resulting bands
at frequencies of
![]()
![]() 0.5MeV. One can see that at
zero frequency cranking around the medium (m) axis gives a
vanishing angular momentum, while those around the other two (s and
l) give non-zero values equal to the s.p. alignments of the odd
proton particle and neutron hole, ss=5.43 and
sl=5.00
0.5MeV. One can see that at
zero frequency cranking around the medium (m) axis gives a
vanishing angular momentum, while those around the other two (s and
l) give non-zero values equal to the s.p. alignments of the odd
proton particle and neutron hole, ss=5.43 and
sl=5.00![]() ,
respectively. For each of the three bands the
dependence of I on
,
respectively. For each of the three bands the
dependence of I on ![]() is linear, like for a rigid rotation,
and the corresponding slopes give the microscopic collective moments
of inertia along the principal axes,
is linear, like for a rigid rotation,
and the corresponding slopes give the microscopic collective moments
of inertia along the principal axes,
![]() ,
,
![]() ,
and
,
and
![]()
![]() /MeV. These values already contain the
contributions,
/MeV. These values already contain the
contributions,
![]() and
and
![]() ,
from the odd
particle and hole.
,
from the odd
particle and hole.
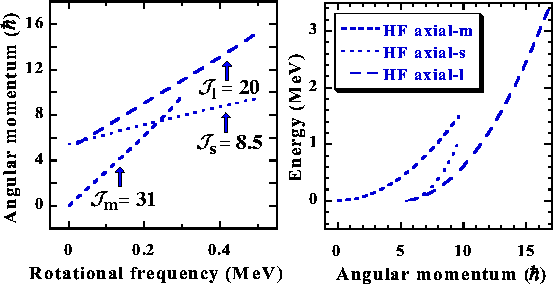 |
The model consists of a triaxial rigid body [10] with two
gyroscopes rigidly fixed along its short and long axes, modeling the
odd nucleons. Moments of inertia
![]() obtained above are the
diagonal components of the body inertia tensor
obtained above are the
diagonal components of the body inertia tensor
![]() ,
which we
otherwise assume diagonal, while
,
which we
otherwise assume diagonal, while
![]() denotes the vector sum
of the gyroscopes' spins.
denotes the vector sum
of the gyroscopes' spins.
The angular momentum of this system reads
![]() .
Here we look only for uniform
rotations, by which we understand that
.
Here we look only for uniform
rotations, by which we understand that
![]() is constant in
the body-fixed frame. In such a case, the Euler equations
[11] take the form
is constant in
the body-fixed frame. In such a case, the Euler equations
[11] take the form
![]() ,
and require
that
,
and require
that
![]() and
and
![]() be parallel, like for the
self-consistent cranking solutions [9]. These equations
can easily be solved. However, to keep contact with the Hartree-Fock
method, here we employ the variational principle to find the
solutions.
be parallel, like for the
self-consistent cranking solutions [9]. These equations
can easily be solved. However, to keep contact with the Hartree-Fock
method, here we employ the variational principle to find the
solutions.
The Lagrangian of the system is equal to the sum of kinetic energies
of the body and gyroscopes [12],
Since the Hamiltonian of the system is
![]() ,
the uniform solutions can be obtained by finding extrema of function
,
the uniform solutions can be obtained by finding extrema of function
![]() which is called Routhian. This serves
as a bridge between our classical model and the quantum cranking
theory where an analogous Routhian is minimized in the space of trial
Slater determinants.
which is called Routhian. This serves
as a bridge between our classical model and the quantum cranking
theory where an analogous Routhian is minimized in the space of trial
Slater determinants.
Extrema of R with respect to the components of
![]() in the
intrinsic frame at a given
in the
intrinsic frame at a given
![]() can be found by using a
Lagrange multiplier
can be found by using a
Lagrange multiplier ![]() for
for
![]() .
Setting to zero the
derivatives of the quantity:
.
Setting to zero the
derivatives of the quantity:
| = | |||
| + | (3) |
Planar solutions: If
![]() then both
then both
![]() and
and
![]() lie in the s-l plane where also the gyroscopes' spins are
located. This gives planar solutions for which the chiral symmetry is
conserved. All values of
lie in the s-l plane where also the gyroscopes' spins are
located. This gives planar solutions for which the chiral symmetry is
conserved. All values of ![]() are allowed, and the Lagrange
multiplier must be determined from the magnitude of
are allowed, and the Lagrange
multiplier must be determined from the magnitude of
![]() .
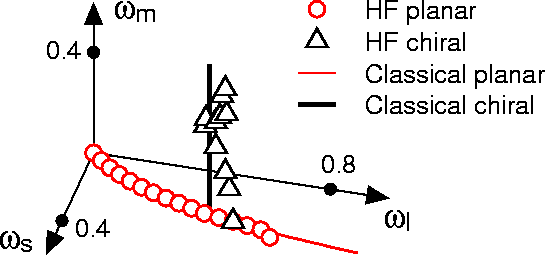
Figure 3 shows
.
Figure 3 shows ![]() versus
versus ![]() for the parameters
extracted from the HF solutions. As can be seen, there always exist
two solutions and above some rotational frequency two more appear.
This threshold frequency reads
for the parameters
extracted from the HF solutions. As can be seen, there always exist
two solutions and above some rotational frequency two more appear.
This threshold frequency reads
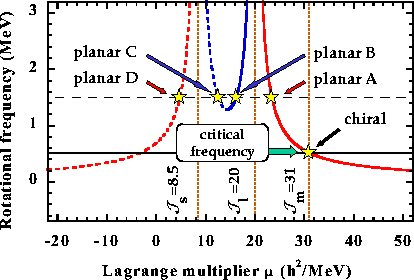 |
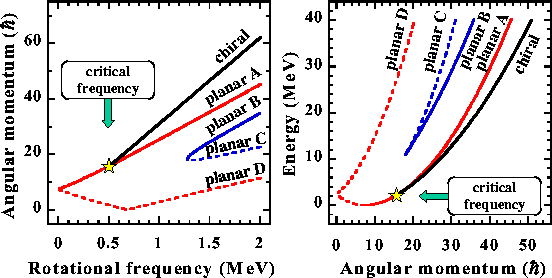
Figure 4 summarizes the angular momenta and energies for
all the bands found in the classical rotor coupled to two gyroscopes.
At low angular momenta, the yrast line coincides with the planar D
band, where the core rotates in the opposite direction as compared to
the gyroscopes. Then it continues along the planar A solution. Since
the moment of inertia
![]() is the largest, beyond the critical
frequency the yrast line coincides with the chiral solution. This may
give us hope of finding chiral bands in experiment.
is the largest, beyond the critical
frequency the yrast line coincides with the chiral solution. This may
give us hope of finding chiral bands in experiment.
We now come back to the microscopic self-consistent HF solutions. By
applying rotational frequency with non-zero s and l components,
we obtained a planar band corresponding to the classical A solution.
At the limit of the zero frequency, the angular momentum is simply a
sum of the contributions from the proton particle and neutron hole,
that are almost equal. Therefore, the initial tilt angle is
approximately equal to
![]() .
With increasing
.
With increasing ![]() ,
the
angular frequency vector
,
the
angular frequency vector
![]() tilts more and more towards
the long axis. At
tilts more and more towards
the long axis. At
![]() =0.75MeV,
=0.75MeV,
![]() is
tilted by
is
tilted by
![]() .
This HF evolution of the tilt angle is to a
very high precision reproduced by our classical model (solid line in
Fig. 5).
.
This HF evolution of the tilt angle is to a
very high precision reproduced by our classical model (solid line in
Fig. 5).
 |
We conclude the presentation of our results by comparing the HF bands
with experimental data[2], Fig. 6. We first
note that the HF critical frequency of
![]() =0.6MeV is significantly higher than the
frequencies at which appear the two experimental bands that are
candidates for the chiral pair[2]. The classical model
gives a clear dependence of
=0.6MeV is significantly higher than the
frequencies at which appear the two experimental bands that are
candidates for the chiral pair[2]. The classical model
gives a clear dependence of
![]() (9) on
the parameters characterizing the system. Therefore, we may speculate
that a smaller critical value can only be obtained by either making
the s.p. alignments (spins of the gyroscopes) smaller, or the
differences of the principal moments of inertia larger.
Inclusion of pairing will probably leave
(9) on
the parameters characterizing the system. Therefore, we may speculate
that a smaller critical value can only be obtained by either making
the s.p. alignments (spins of the gyroscopes) smaller, or the
differences of the principal moments of inertia larger.
Inclusion of pairing will probably leave
![]() unchanged (blocked
states), and at the same time decrease the moments of inertia, thus
rendering
unchanged (blocked
states), and at the same time decrease the moments of inertia, thus
rendering
![]() possibly even higher. Only making
the deformation parameter
possibly even higher. Only making
the deformation parameter ![]() closer to
closer to
![]() ,
could,
according to the hydrodynamical model [5], decrease the
differences of the diagonal moments of inertia and make
,
could,
according to the hydrodynamical model [5], decrease the
differences of the diagonal moments of inertia and make
![]() lower. A case with
lower. A case with
![]() was
considered in Ref. [4].
was
considered in Ref. [4].
 |
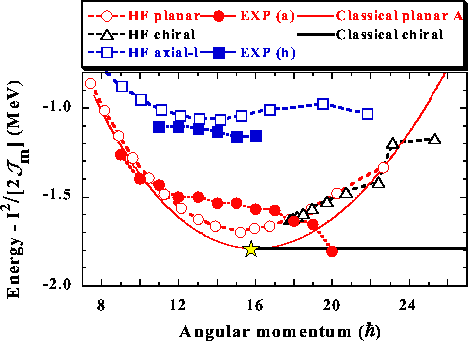 |
In summary, solutions corresponding to the planar and chiral nuclear bands were found for the first time within a fully self-consistent microscopic approach. We have shown that most of the characteristics of the HF solutions can be analyzed in terms of a simple model describing rotation of a triaxial body coupled to two gyroscopes. In particular, the model gives an analytic expression for the value of the critical angular frequency at which the chiral band begins. This value seems to be rather high as compared to the angular frequencies corresponding to the pair of experimental bands in 132La, where the existence of a chiral pair was suggested. A tentative interpretation of the experimental bands as those exhibiting a planar and axial-l rotations was possible.
Interesting comments by W. Nazarewicz and K. Starosta are gratefully acknowledged. This research was supported in part by the Polish Committee for Scientific Research (KBN) under Contract No. 5 P03B 014 21, by the French-Polish integrated actions program POLONIUM, and by the computational grant from the Interdisciplinary Centre for Mathematical and Computational Modeling (ICM) of the Warsaw University.