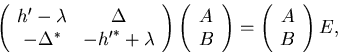 |
(6) |
In order to incorporate pairing correlations for rotating states,
the new version (v2.07f) of the code HFODD
solves the standard HFB equation [10],
For the conserved simplex symmetry, which in the present version is assumed
when solving the HFB equation, the Routhian and the pairing
potential acquire the following block forms [12,10]:
For the conserved time-reversal symmetry, diagonal matrices of
eigenvalues ![]() and
and ![]() are identical to one another, and
the separation of eigenvectors of Eq. (8) into
two simplexes is trivial; it is enough to group positive and negative
quasiparticle energies together. For broken time-reversal this
procedure does not work, because there can be more than half positive
or negative quasiparticle energies in the spectrum of Eq. (8). So in general one has to put the half of largest
eigenvalues into matrix
are identical to one another, and
the separation of eigenvectors of Eq. (8) into
two simplexes is trivial; it is enough to group positive and negative
quasiparticle energies together. For broken time-reversal this
procedure does not work, because there can be more than half positive
or negative quasiparticle energies in the spectrum of Eq. (8). So in general one has to put the half of largest
eigenvalues into matrix ![]() , and the half of smallest into matrix
, and the half of smallest into matrix
![]() , irrespective of their signs. Such a choice leads to the
solution that corresponds to the so-called quasiparticle vacuum.
, irrespective of their signs. Such a choice leads to the
solution that corresponds to the so-called quasiparticle vacuum.
Based on the solution of the matrix equation (8), we have
upper and lower components of the quasiparticle wave functions in
the space coordinates as
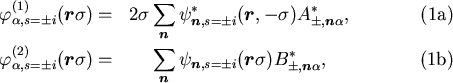 where
where
![]() are the HO simplex
wave functions (I-78) in space coordinates (I-76) and
are the HO simplex
wave functions (I-78) in space coordinates (I-76) and
![]() =
=![]() are the numbers of the HO quanta in three
Cartesian directions. In Eq. (10) we have used the fact
that the s.p. basis states of either of the two simplexes,
are the numbers of the HO quanta in three
Cartesian directions. In Eq. (10) we have used the fact
that the s.p. basis states of either of the two simplexes,
![]() , can be numbered by the HO quantum numbers
, can be numbered by the HO quantum numbers
![]() . We
have also introduced index
. We
have also introduced index ![]() =1,...,
=1,...,![]() , which numbers
eigenstates of Eq. (8) in both "halfs" of the spectrum
defined above.
, which numbers
eigenstates of Eq. (8) in both "halfs" of the spectrum
defined above.
From the quasiparticle wave functions we obtain the standard particle and
pairing density matrices [13],
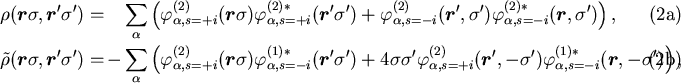 where the sum over
where the sum over ![]() is performed up to the maximum
equivalent-spectrum energy
is performed up to the maximum
equivalent-spectrum energy
![]() , see Ref. [14]
for details.
All particle-hole mean-field potentials can be calculated from
the particle density matrix
, see Ref. [14]
for details.
All particle-hole mean-field potentials can be calculated from
the particle density matrix
![]() and its derivatives (see I), while the particle-particle mean-field
potentials can be calculated from the pairing density matrix
and its derivatives (see I), while the particle-particle mean-field
potentials can be calculated from the pairing density matrix
![]() [13]. In
the present implementation of the code HFODD, terms depending on
derivatives of the particle-particle density matrix are not taken
into account, and hence the pairing potential depends only on the
local pair density
[13]. In
the present implementation of the code HFODD, terms depending on
derivatives of the particle-particle density matrix are not taken
into account, and hence the pairing potential depends only on the
local pair density
Finally, matrix elements of the pairing potential in the simplex HO
basis, which are needed in Eq. (8), can be calculated
in exactly the same way as matrix elements of the central mean-field
potential,
Sec. I-4.2, i.e.,