


Next: Constraints for the vector-isovector
Up: Continuity equation and local
Previous: Constraints for the scalar-isovector
Constraints for the vector-isoscalar channel (fourth and sixth orders)
At fourth order, we again found two identical sets of linear
combinations of the isoscalar and isovector coupling constants, in which
the scalar and vector coupling constants are in same case connected
to one another, that is,
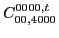 |
 |
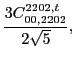 |
(113) |
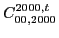 |
 |
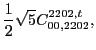 |
(114) |
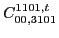 |
 |
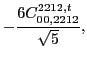 |
(115) |
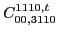 |
 |
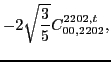 |
(116) |
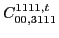 |
 |
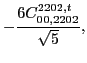 |
(117) |
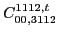 |
 |
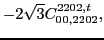 |
(118) |
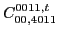 |
 |
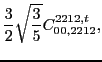 |
(119) |
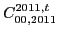 |
 |
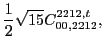 |
(120) |
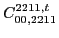 |
 |
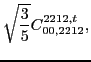 |
(121) |
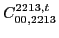 |
 |
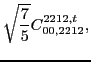 |
(122) |
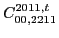 |
 |
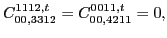 |
(123) |
with the two coupling constants
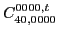 left unrestricted.
Apart from these 6 free and 20 dependent coupling constants, the
vector-isoscalar channel of the CE requires that all the remaining
fourth-order coupling constants are forced to be equal to zero. In particular
in the Eq. (123) we showed the vanishing coupling constants,
belonging to the set of ones with indices
left unrestricted.
Apart from these 6 free and 20 dependent coupling constants, the
vector-isoscalar channel of the CE requires that all the remaining
fourth-order coupling constants are forced to be equal to zero. In particular
in the Eq. (123) we showed the vanishing coupling constants,
belonging to the set of ones with indices 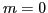 and
and 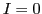 , which were found
to be non-vanishing in the scalar-isoscalar channel.
, which were found
to be non-vanishing in the scalar-isoscalar channel.
At sixth order the pattern of the results is the same, and we have,
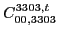 |
 |
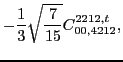 |
(124) |
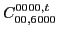 |
 |
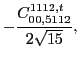 |
(125) |
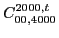 |
 |
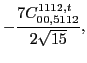 |
(126) |
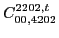 |
 |
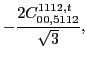 |
(127) |
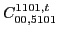 |
 |
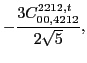 |
(128) |
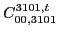 |
 |
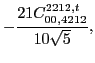 |
(129) |
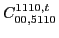 |
 |
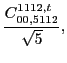 |
(130) |
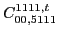 |
 |
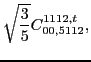 |
(131) |
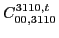 |
 |
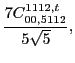 |
(132) |
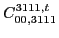 |
 |
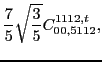 |
(133) |
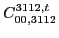 |
 |
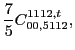 |
(134) |
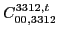 |
 |
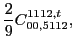 |
(135) |
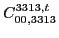 |
 |
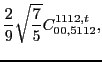 |
(136) |
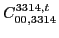 |
 |
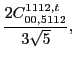 |
(137) |
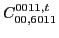 |
 |
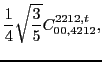 |
(138) |
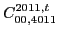 |
 |
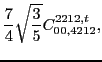 |
(139) |
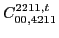 |
 |
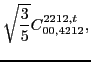 |
(140) |
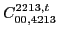 |
 |
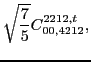 |
(141) |
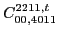 |
 |
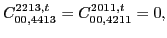 |
(142) |
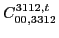 |
 |
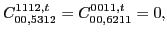 |
(143) |
with the two coupling constants
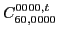 left unrestricted.
Apart from these 6 free and 36 dependent coupling constants, the
vector-isoscalar channel of the CE requires that all the remaining
sixth-order coupling constants are forced to be equal to zero. As before, we
listed explicitely the vanishing coupling constants (see Eqs. (142)-(143)),
which were found
to be non-vanishing in the scalar-isoscalar channel.
left unrestricted.
Apart from these 6 free and 36 dependent coupling constants, the
vector-isoscalar channel of the CE requires that all the remaining
sixth-order coupling constants are forced to be equal to zero. As before, we
listed explicitely the vanishing coupling constants (see Eqs. (142)-(143)),
which were found
to be non-vanishing in the scalar-isoscalar channel.
The general rule that we have specified at the end of the
Appendix A, can be applied now to explain
the results of this section, where at all the orders we found
constraints that are nondiagonal in the spin space. Here, the reason
is the possibility of having pairs of secondary densities that are
coupled to rank 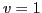 . These pairs can appear at both scalar and
vector coupling constants, which results in relating them to one
another.
. These pairs can appear at both scalar and
vector coupling constants, which results in relating them to one
another.



Next: Constraints for the vector-isovector
Up: Continuity equation and local
Previous: Constraints for the scalar-isovector
Jacek Dobaczewski
2011-11-11
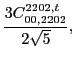
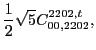
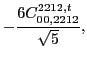
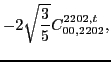
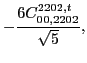
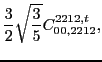
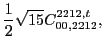
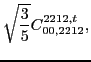
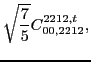
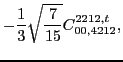
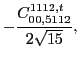
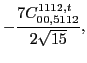
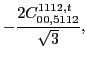
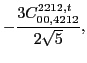
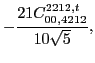
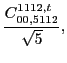
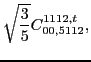
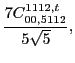
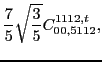
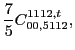
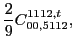
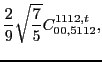
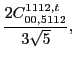
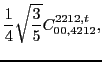
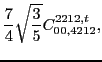
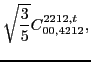
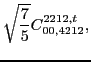
![]() . These pairs can appear at both scalar and
vector coupling constants, which results in relating them to one
another.
. These pairs can appear at both scalar and
vector coupling constants, which results in relating them to one
another.