At fourth order we found that the isoscalar and isovector coupling
constants are connected or not depending on the parity of quantum
numbers ![]() . Moreover, similarly as for the scalar-isoscalar channel of the CE,
the scalar and vector coupling constants are kept apart. The
constraints among the scalar coupling constants read,
. Moreover, similarly as for the scalar-isoscalar channel of the CE,
the scalar and vector coupling constants are kept apart. The
constraints among the scalar coupling constants read,
We also found that the fourth-order surface isovector coupling constants
must vanish,
In the same way, at sixth order we found the following constraints for
the scalar,
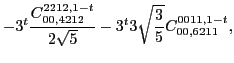 |
(94) | ||
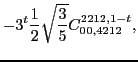 |
(95) | ||
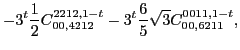 |
(96) | ||
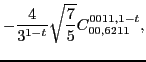 |
(97) | ||
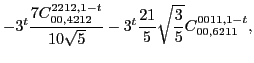 |
(98) | ||
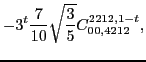 |
(99) | ||
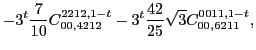 |
(100) | ||
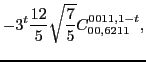 |
(101) | ||
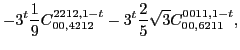 |
(102) | ||
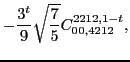 |
(103) | ||
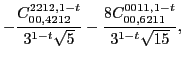 |
(104) | ||
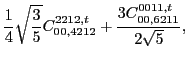 |
(105) | ||
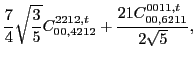 |
(106) | ||
| (107) | |||
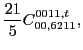 |
(108) | ||
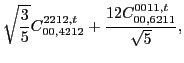 |
(109) | ||
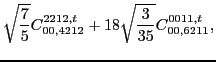 |
(110) | ||
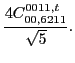 |
(111) |
We also found that the sixth-order surface isovector coupling constants
must vanish,
We have seen that for the scalar-isovector channel, the coupling
constants are diagonal or nondiagonal in the isospin quantum number
![]() . We can understand this point considering the fact that in order
to separate the scalar-isovector channel of the CE and obtain
condition (48) for
. We can understand this point considering the fact that in order
to separate the scalar-isovector channel of the CE and obtain
condition (48) for ![]() , we have to multiply
Eq. (41) by the isospin operator
, we have to multiply
Eq. (41) by the isospin operator
![]() . Then, the
isospin index
. Then, the
isospin index ![]() tells us in which half of the isospin
space the coupling constants is. Nondiagonal constraints mean, in
fact, that the same pair of secondary densities in the final form of
condition (48) can be produced by two terms of the
functional that are isoscalar and isovector. This
is possible, because the coupling to rank
tells us in which half of the isospin
space the coupling constants is. Nondiagonal constraints mean, in
fact, that the same pair of secondary densities in the final form of
condition (48) can be produced by two terms of the
functional that are isoscalar and isovector. This
is possible, because the coupling to rank ![]() allows for pairs
of densities nondiagonal in the isospin space, and this, in turn, boils
down to constraints for coupling constants nondiagonal in the isospin space.
allows for pairs
of densities nondiagonal in the isospin space, and this, in turn, boils
down to constraints for coupling constants nondiagonal in the isospin space.