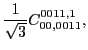 |
(51) | ||
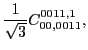 |
(52) |
For zero-order terms, condition (48) gives no constraints
on the coupling constants, apart from those in the vector-isovector
channel, where we have,
It is interesting to discuss these results in connection with the
derivation of the CE for a spin-
![]() particle moving in a local
potential, which we gave in Sec. 2.1. There, we
pointed out that the CE in the vector channel is valid when the
vector potential is parallel to the spin density. Exactly this
situation occurs for the zero-order EDF, where in each spin-isospin
channel the potential functions are simply proportional to densities.
particle moving in a local
potential, which we gave in Sec. 2.1. There, we
pointed out that the CE in the vector channel is valid when the
vector potential is parallel to the spin density. Exactly this
situation occurs for the zero-order EDF, where in each spin-isospin
channel the potential functions are simply proportional to densities.
In fact, the simple algebraic rule of the vector product in
Eq. (5) is equivalent to the coupling of pairs of
identical commuting rank 1 tensors to rank 1, which is identically
null. This is just the case for the coupling to rank ![]() (
(![]() ) in
the spin (isospin) space for the vector-isoscalar (scalar-isovector)
channel of the CE, in which the identically null tensors formed by
the pairs of densities at zero order leave the corresponding coupling
constants unrestricted. However, when the coupling to a rank-1 tensor
is simultaneously performed in both spin and isospin space (
) in
the spin (isospin) space for the vector-isoscalar (scalar-isovector)
channel of the CE, in which the identically null tensors formed by
the pairs of densities at zero order leave the corresponding coupling
constants unrestricted. However, when the coupling to a rank-1 tensor
is simultaneously performed in both spin and isospin space (![]() and
and
![]() ), as is the case in the vector-isovector channel of the CE, the
two negative signs in the commutation of the pair of densities give
an overall positive sign, and the above selection rule does not
apply. This explains why, at zero order of the vector-isovector
channel, condition (48) does induce constraints on
coupling constants - those given in Eqs. (51) and
(52).
), as is the case in the vector-isovector channel of the CE, the
two negative signs in the commutation of the pair of densities give
an overall positive sign, and the above selection rule does not
apply. This explains why, at zero order of the vector-isovector
channel, condition (48) does induce constraints on
coupling constants - those given in Eqs. (51) and
(52).