Next: Zero-order (LO) EDF. Up: General form of the Previous: Finite-range pseudopotential with higher-order
The interaction energy, which is the potential part of the EDF, is
derived by averaging the pseudopotential ![]() (2) over the
uncorrelated nuclear wave function expressed as Slater determinant.
The functional obtained in this way is in general nonlocal, meaning
that it contains terms depending on one-body densities
non-diagonal with respect to the spatial coordinates.
(2) over the
uncorrelated nuclear wave function expressed as Slater determinant.
The functional obtained in this way is in general nonlocal, meaning
that it contains terms depending on one-body densities
non-diagonal with respect to the spatial coordinates.
If we leave out the exchange operator from the
pseudopotential (2), we can define it as
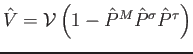 . This allows us to
express the EDF in the following way,
. This allows us to
express the EDF in the following way,
We performed derivations of average energies (7)
separately for all terms of the pseudopotential (2).
The final result of this derivation is given by linear
combinations of terms of the EDF appearing on the rhs of the
following expression,
The formalism developed in Ref. [9], along with the
straightforward extension to the isospace introduced in
Ref. [12], which originally pertained to quasilocal
higher-order EDF and zero-range pseudopotential, can easily be
accommodated to express the EDF discussed in this paper. Then, direct (local) terms
of the functional, bilinear in local densities, read
In an analogous way, exchange (nonlocal) terms of the functional read
The coupling constants of the functional that we consider in the
present study do not depend on densities. Therefore, in principle, in
expressions (10) and
(12) one could perform
integrations by parts and thus, in an attempt to achieve the same
form as that for the quasilocal EDF considered in
Ref. [9], transfer the derivative operators ![]() onto
the second density. However, this transformation would have created a
series of extra terms produced by the action of the derivative
operators onto the regularized delta, in such a way that the
functional would have had a mixed form composed of derivatives of
densities and an expansion in the parameter
onto
the second density. However, this transformation would have created a
series of extra terms produced by the action of the derivative
operators onto the regularized delta, in such a way that the
functional would have had a mixed form composed of derivatives of
densities and an expansion in the parameter ![]() of (1).
For this reason, we keep the form of
Eqs. (10)
and (12) with the derivatives
operators acting on both densities.
of (1).
For this reason, we keep the form of
Eqs. (10)
and (12) with the derivatives
operators acting on both densities.
Explicit
calculations of linear combinations in Eq. (9)
are formally identical to those performed for the
zero-range pseudopotential (see Sec. III of Ref. [11] for
details). In this Section, we present general results for the
finite-range pseudopotential (2), which we also supplement
by those pertaining to the symmetric spin-saturated nuclear matter.
Table 2 lists the numbers of independent
terms (10)
and (12) of the functional
obtained from the finite-range pseudopotential. Each allowed
combination of indexes (
![]() ) gives a pair of
EDF terms, one local and another one nonlocal; therefore, the numbers shown
are twice the numbers of such allowed combinations. The fact that the
isospin does not couple with operators belonging to spin and
position-coordinate space, along with the requirement that the EDF is
isoscalar, implies that isoscalar and isovector densities,
respectively
) gives a pair of
EDF terms, one local and another one nonlocal; therefore, the numbers shown
are twice the numbers of such allowed combinations. The fact that the
isospin does not couple with operators belonging to spin and
position-coordinate space, along with the requirement that the EDF is
isoscalar, implies that isoscalar and isovector densities,
respectively ![]() =0 and
=0 and ![]() =1,
give rise to two isospin channels in the
functional having the same structure. Therefore only one isospin
channel is accounted for in Table 2. For the symmetric nuclear
matter, the isovector terms
do not contribute.
=1,
give rise to two isospin channels in the
functional having the same structure. Therefore only one isospin
channel is accounted for in Table 2. For the symmetric nuclear
matter, the isovector terms
do not contribute.
Table 2 also displays numbers of EDF
independent terms obtained separately from the central
(![]() =0), SO (
=0), SO (![]() =1), and tensor (
=1), and tensor (![]() =2) terms of the
finite-range pseudopotential. Strictly speaking, the EDF cannot be
divided into central and tensor contributions, even though the SO
part of the EDF is decoupled from the other two. This is at
the origin of the functional terms that mix scalar and vector densities in
spin spaces. However there are terms of the EDF that can be produced by
both central and tensor terms of the pseudopotential. This explains
why the sums of terms in the second, third, and fourth columns do not
equal to the corresponding values in the fifth column.
=2) terms of the
finite-range pseudopotential. Strictly speaking, the EDF cannot be
divided into central and tensor contributions, even though the SO
part of the EDF is decoupled from the other two. This is at
the origin of the functional terms that mix scalar and vector densities in
spin spaces. However there are terms of the EDF that can be produced by
both central and tensor terms of the pseudopotential. This explains
why the sums of terms in the second, third, and fourth columns do not
equal to the corresponding values in the fifth column.
| Order | Total | Nuclear matter | ||||
| 0 | 4 | 0 | 0 | 4 | 2 | |
| 2 | 24 | 8 | 16 | 36 | 3 | |
| 4 | 144 | 64 | 114 | 222 | 8 | |
| 6 | 640 | 336 | 564 | 1010 | 12 | |
| N |
776 | 408 | 694 | 1272 | 25 |