Finite-range pseudopotential with higher-order momenta

The pseudopotential that we introduce here can be regarded as a common extension of the most successful nuclear phenomenological interactions: the Skyrme and Gogny forces. Indeed, the central part of our pseudopotential is finite-range and momentum-dependent, whereas the one of the Skyrme force is momentum-dependent but zero-range and the one of the Gogny force is finite-range but momentum-independent. Similarly as for the Skyrme force, we build the pseudopotential in terms of an expansion in relative momenta, and similarly as for the Gogny force, we use finite-range formfactors. We note here that the constructed pseudopotential has only one finite-range parameter, allowing us to interpret that parameter as a regularization scale, according to the ET philosophy [3].

Following closely the methodology of introducing higher-order derivatives of zero-range pseudopotentials [11], we obtain the general form of the finite-range pseudopotential by coupling derivative operators with spin operators in the spherical-tensor formalism. The complete list of the building blocks of the tensors can be found in Ref. [9]. We obtain the finite-range version by simply substituting the zero-range Dirac delta with a regularized (smeared) delta,

$$g_a(\bm{r})=g_a(r)= \frac{e^{-\frac{r^2}{a^2}}}{\left(a\sqrt{\pi}\right)^3} ,$$ (1)

where $r=\vert\bm{r}\vert=\vert\bm{r}_2-\bm{r}_1\vert$ and $\bm{r}_2$ and $\bm{r}_1$ are positions of the two interacting particles.

In such a formalism, the general expression for the antisymmetrized finite-range pseudopotential reads,

$$\hat{V}=\sum_{\tilde{n}' \tilde{L}', \tilde{t} \atop \ti... ...e{L},v_{12} \tilde{S}}^{\tilde{n}' \tilde{L}', \tilde{t} } ,$$ (2)

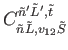where each term, which is built according to the symmetries discussed in Ref. [11] and multiplied by the corresponding strength parameter $C_{\tilde{n} \tilde{L},v_{12} \tilde{S}}^{\tilde{n}' \tilde{L}', \tilde{t} }$, is given by

$$\hat{V}_{\tilde{n} \tilde{L},v_{12} \tilde{S}}^{\tilde{n}' \tilde{L}', \tilde{t} }= \frac{1}{2}i^{v_{12}} \left( \left[ \left[K'_{\tilde{n}'\tilde{L}... ...{L}}\right]_{\tilde{S}} \hat{S}_{v_{12} \tilde{S}}\right]_{0} \right. \nonumber$$

$$\left. + (-1)^{v_{12}+\tilde{S}} \left[ \left[K'_{\tilde{n} \tild... ..._{v_{12} \tilde{S}}\right]_{0} \right)\left(\hat{P}^{\tau}\right)^{ \tilde{t} }$$

$$\times \left(1-\hat{P}^{M}\hat{P}^{\sigma}\hat{P}^{\tau}\right) \delta(\bm{r}'_1\!-\! \bm{r}_1) \delta(\bm{r}'_2\!-\! \bm{r}_2) g_a(r) .$$ (3)

For the sake of completeness, we recall here definitions of tensors that appear in Eq. (3). Each term of the pseudopotential is a scalar with a composite internal structure and is built of higher-rank spherical tensors in the space, spin, and isospin coordinates. Higher-order tensor derivatives $K_ {\tilde{n }\tilde{L}}$ are built of relative momenta $\bm{k}=(\bm{\nabla}_1-\bm{\nabla}_2)/2i$, with spherical components

$$k_{1,\mu=\left\{-1,0,1\right\}} = -i \left\{{\textstyle... ...extstyle{\frac{-1}{\sqrt{2}}}}\left(k_x+ik_y\right)\right\} ,$$ (4)

that are coupled to rank $\tilde{L}$, where symbol $\tilde{n}$ denotes the order of the tensor, that is, the number of operators $\bm{k}$. Operators acting on the primed coordinates, $K'_{\tilde{n} \tilde{L}}$, are built in the same way of relative momenta $\bm{k}'=(\bm{\nabla}'_1-\bm{\nabla}'_2)/2i$.

In the spin space, for particles numbered by $i=$1 or 2, we have as building blocks the spin unity matrix of rank 0, denoted as $\sigma^{(i)}_{00}$, and the Pauli matrices $\sigma^{(i)}_{ x,y,z}$, which define the spin spherical tensor of rank 1,

$$\sigma^{(i)}_{ 1,\mu=\left\{-1,0,1\right\}} = -i \left\... ...\left(\sigma^{(i)}_{ x} +i\sigma^{(i)}_{ y}\right)\right\}.$$ (5)

From these definitions, we can construct tensors of rank up to 2, according to the following symmetrized expression

$$\hat{S}_{v_{12} \tilde{S}} =\left(1-{\textstyle{\frac{1}{2}}}\del... ...v_2}]_{\tilde{S}} + [\sigma^{(1)}_{v_2}\sigma^{(2)}_{v_1}]_{\tilde{S}} \right),$$ (6)

where $v_{12}=v_1+v_2$ and $\sigma^{(i)}_{v}$ are the spherical-tensor rank-$v$ Pauli matrices.

The locality delta functions $\delta(\bm{r}'_1\!-\! \bm{r}_1)\delta(\bm{r}'_2\!-\! \bm{r}_2)$ together with the regularized delta $g_a(r)$ must be understood as distributions, whereupon the derivatives in $K_ {\tilde{n }\tilde{L}}$ and $K'_{\tilde{n} \tilde{L}}$ act. The locality deltas ensure the locality of the energy density only in the zero-range case, whereas it is in principle nonlocal due to the presence of the so called Majorana operator $\hat{P}^{M}$ in the exchange part of the pseudopotential.

In Eq. (3), index $\tilde{t}$, taking either value 0 or 1, defines the dependence of the pseudopotential on the isospin. This dependence is in addition to that stemming from the exchange term, and is a new element as compared to the case of the zero-range pseudopotential [11].

In principle, one could write down an equivalent version of the antisymmetrized finite-range pseudopotential, where the new dependence on the isospin exchange operator would have been substituted by the Majorana operator exchanging space coordinates, $\hat{P}^{M}$. This would be possible in virtue of the relation $\hat{P}^{\tau}\equiv-\hat{P}^{\sigma}\hat{P}^{M}$, valid when acting on a fermionic wave function. However, the presence of the Majorana operator in the pseudopotential would break the correspondence between the exchange part of the antisymmetrized pseudopotential and the nonlocal sector of the EDF, according to the common understanding of the nonlocal part of the EDF as resulting from the exchange part of the antisymmetrized interaction. While in a zero-range pseudopotential this operator reduces to a phase depending on the order of the relative-momenta tensors [23,11], in a finite-range interaction this operator acts explicitly, and switches the space coordinates of the two interacting nucleons. Therefore the finite-range character of the interaction, complemented with the action of the Majorana operator, would have given rise to the nonlocal form of the functional stemming from the direct interaction. Although such a construction would be perfectly correct and exactly equivalent to that presented below, it would also be counterintuitive, and thus in our study it is not further pursued.

The constructed pseudopotential possesses all symmetries of the nuclear interaction. Referring the reader to Ref. [11] for a comprehensive discussion, here we only list these symmetries, which are rotational symmetry, time-reversal, parity, and Galilean invariance, supplemented with the hermiticity of the pseudopotential operator and indistinguishability principle operating as invariance under exchange of particles 1 and 2. The pseudopotential (2) is indeed invariant under all the transformations corresponding to the symmetries listed above. This guarantees that the resulting EDF is also invariant with respect to the same symmetries.

All terms of the pseudopotential, derived at zero, second, fourth, and sixth order, $\tilde{n}+\tilde{n}'=0$, 2, 4, and 6, respectively, are collected in the supplemental material. The supplemental material contains all detailed results of the present study. They were derived by means of symbolic programing, and are presented in readable format as well as in the form directly usable in computer programming. In Table 1 we show numbers of different terms of pseudopotential (2), where we also distinguish between central ($\tilde{S}=0$), SO ($\tilde{S}=1$), and tensor ($\tilde{S}=2$) terms, corresponding to different ranks in the coupling of the relative momenta tensors $K_ {\tilde{n }\tilde{L}}$ with the spin operator $\hat{S}_{v_{12} \tilde{S}}$. At each order, the overall numbers of terms equal 4, 14, 30, and 52, giving the total number of 100 terms up to N$^3$LO. At each order, these numbers are twice larger than the corresponding numbers for the zero-range pseudopotential, which reflects the addition of the new quantum number $\tilde{t}$.

We note, that here we classified tensor terms as those corresponding to $\tilde{S}=2$; however, in the pseudopotential (3) there also appear terms that have purely space-tensor character, e.g., those for $\tilde{S}=0$ and $\tilde{L}=\tilde{L}'=2$. However, we know from the generalized Cayley-Hamilton (GCH) theorem [24], that any scalar function of two vectors $\bm{k}$ and $\bm{k}'$ must have form of a function of three elementary scalars $\bm{k}^2$, $\bm{k}'^2$, and $\bm{k}'\cdot\bm{k}$. Therefore, the central term ($\tilde{S}=0$) can always be recoupled to the form where terms with $\tilde{L},\tilde{L}'>1$ do not appear. An explicit construction of such a form is presented in the Cartesian coordinates in Sec. 4.

Table 1: Numbers of terms of pseudopotential (2) at different orders up to N$^3$LO. In the second, third, and fourth column, numbers of central ($\tilde{S}=0$), SO ($\tilde{S}=1$), and tensor ($\tilde{S}=2$) terms, respectively, are displayed.

	Order	$\tilde{S}=0$	$\tilde{S}=1$	$\tilde{S}=2$	Total
	0	4	0	0	4
	2	8	2	4	14
	4	16	4	10	30
	6	24	8	20	52
	N$^3$LO	52	14	34	100