


Next: Regularization of the pairing
Up: Examples
Previous: Examples
Self-consistent calculation for 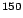 Sn
Sn
As a first example we discuss here the results obtained for
the semi magic isotope 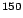 Sn (
Sn (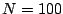 and
and 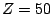 )
using the effective force SLy4
)
using the effective force SLy4
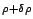 .
This
nucleus is an interesting example since it has a rather small
neutron Fermi energy (
.
This
nucleus is an interesting example since it has a rather small
neutron Fermi energy (
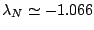 MeV).
Small neutron separation energy allows us to discuss
possible effects of the integration box size as well as
the choice of the boundary condition.
If not explicitly stated otherwise, in all calculations the
integration step is
MeV).
Small neutron separation energy allows us to discuss
possible effects of the integration box size as well as
the choice of the boundary condition.
If not explicitly stated otherwise, in all calculations the
integration step is 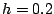 fm
for the box size of
fm
for the box size of
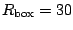 fm, i.e., the number of
integration points is 150+1.
The global properties
of the nucleus for Dirichlet or Neumann boundary
condition are shown in table 5.
fm, i.e., the number of
integration points is 150+1.
The global properties
of the nucleus for Dirichlet or Neumann boundary
condition are shown in table 5.
Table 5:
Total binding energy, mean pairing gap, Fermi energy (all in MeV)
and neutron rms radius (in fm) in 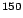 Sn, calculated for the force
SLy4
Sn, calculated for the force
SLy4
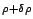 and two different
boundary conditions: Dirichlet (vanishing wave functions
at
and two different
boundary conditions: Dirichlet (vanishing wave functions
at
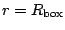 ) or Neumann (vanishing derivative of
the wave functions at
) or Neumann (vanishing derivative of
the wave functions at
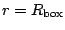 ).
).
| Boundary condition |
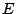 |
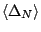 |
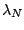 |
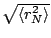 |
| Dirichlet |
-1131.863 |
-1.431 |
-1.067 |
5.264 |
| Neumann |
-1131.862 |
-1.431 |
-1.067 |
5.264 |
|
In addition to the small neutron separation energy,
one finds several single particle states with a significant
occupation around 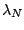 with different values of
with different values of 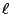 and indeed different asymptotic
bahaviour. The single particle neutron states in the vicinity
of the Fermi energy are shown in table 6. It is
gratifying to observe that despite the fact that the quasiparticle
states are a little bit influenced by the change of the boundary
conditions, the canonical states remain unchanged.
and indeed different asymptotic
bahaviour. The single particle neutron states in the vicinity
of the Fermi energy are shown in table 6. It is
gratifying to observe that despite the fact that the quasiparticle
states are a little bit influenced by the change of the boundary
conditions, the canonical states remain unchanged.
Table:
Single particle neutron levels in 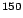 Sn using the
effective force SLy4
Sn using the
effective force SLy4
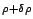 . Calculations
have been made in a 30fm box with an integration step of
0.2fm.
. Calculations
have been made in a 30fm box with an integration step of
0.2fm. 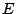 and
and 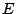 are the quasiparticle energies
and norms of the lower components while
are the quasiparticle energies
and norms of the lower components while
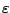 is
the canonical energy (54) and
is
the canonical energy (54) and 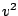 is the occupation
factor of the corresponding canonical state (55).
is the occupation
factor of the corresponding canonical state (55).
| Boundary condition |
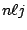 |
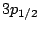 |
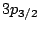 |
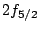 |
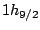 |
| Dirichlet |
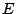 (MeV) (MeV) |
0.926 |
0.937 |
1.330 |
1.556 |
| |
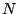 |
0.221 |
0.577 |
0.254 |
0.438 |
| |
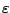 (MeV) (MeV) |
1.169 |
1.051 |
1.445 |
1.572 |
| |
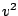 |
0.251 |
0.619 |
0.264 |
0.438 |
| Neumann |
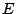 (MeV) (MeV) |
0.919 |
0.932 |
1.328 |
1.556 |
| |
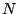 |
0.211 |
0.562 |
0.251 |
0.438 |
| |
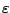 (MeV) (MeV) |
1.168 |
1.051 |
1.445 |
1.572 |
| |
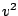 |
0.251 |
0.619 |
0.263 |
0.438 |
|
When a rather exotic nucleus is studied, it is important
to check how well the results are converged with respect to
the various approximations which are made in the numerical
treatment of the HFB problem. First of all, we limit the
calculation to a maximum number of partial wave given
by
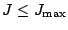 , which has to by consistent with the
mass of the nucleus.
The convergence of the kinetic, pairing,
and total energies are shown in the left part of Fig. 2.
Between
, which has to by consistent with the
mass of the nucleus.
The convergence of the kinetic, pairing,
and total energies are shown in the left part of Fig. 2.
Between
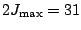 and 37 the total energy
difference is 1.3keV.
The changes in the kinetic and pairing energies are a little
bit bigger (7keV and 6keV, respectively); since these
quantities are not at their extrema,
they react more rapidly to a small change of the wave function.
and 37 the total energy
difference is 1.3keV.
The changes in the kinetic and pairing energies are a little
bit bigger (7keV and 6keV, respectively); since these
quantities are not at their extrema,
they react more rapidly to a small change of the wave function.
Figure 2:
Kinetic (top panels), pairing (middle panels) and
total energies (lower panels) for 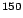 Sn as functions
of
Sn as functions
of
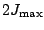 in a 30 fm box with an integration step of
0.2 fm (left) and
of the pairing-field cut-off radius
in a 30 fm box with an integration step of
0.2 fm (left) and
of the pairing-field cut-off radius
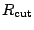 defined
in Eq. (77) (right).
defined
in Eq. (77) (right).
|
|
As discussed in section 5.3, the introduction of
the cut-off radius
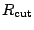 in the pairing channel,
Eq. (77), can improve
the numerical stability of the iterative procedure when
solving the HFB equation. The right part of Figure 2
displays the evolution of the kinetic, pairing, and total
energies with the same parameters as in the left part of the
Figure, except for the value of
in the pairing channel,
Eq. (77), can improve
the numerical stability of the iterative procedure when
solving the HFB equation. The right part of Figure 2
displays the evolution of the kinetic, pairing, and total
energies with the same parameters as in the left part of the
Figure, except for the value of
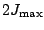 which is fixed at 31. It can
be clearly seen that beyond a rather small distance, the total energy
and its components are not affected by the introduction of this
cut-off. Specifically, for
which is fixed at 31. It can
be clearly seen that beyond a rather small distance, the total energy
and its components are not affected by the introduction of this
cut-off. Specifically, for
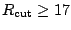 fm the change in
the total energy is less than 0.001keV.
fm the change in
the total energy is less than 0.001keV.
Figure 3:
Difference between the total
energy 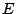 of
of  Sn (solid line) and its average asymptotic value
Sn (solid line) and its average asymptotic value 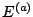 (see text) as a function
of the box size
(see text) as a function
of the box size
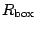 , and the analogous difference for
the two-neutron separation energy
, and the analogous difference for
the two-neutron separation energy 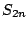 (dashed line).
(dashed line).
|
|
Figure 3 shows the convergence of the total energy 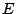 and two-neutron separation energy
and two-neutron separation energy 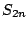 as functions of the
size of the box. Calculations have been made for
as functions of the
size of the box. Calculations have been made for
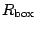 ranging
from 10 fm to 60 fm with a step of 0.4 fm. The cut-off equivalent energy of
ranging
from 10 fm to 60 fm with a step of 0.4 fm. The cut-off equivalent energy of
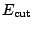 =60MeV and the diffuseness of 1MeV have been used.
In order to clearly exhibit the asymptotic trend of these
quantities we have estimated their average asymptotic values
=60MeV and the diffuseness of 1MeV have been used.
In order to clearly exhibit the asymptotic trend of these
quantities we have estimated their average asymptotic values
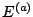 and
and
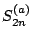 .
Since for
.
Since for
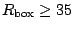 fm
the results
do not show any significant evolution, these values are
estimated by taking averages
for 35 fm
fm
the results
do not show any significant evolution, these values are
estimated by taking averages
for 35 fm
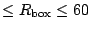 fm, which gives
fm, which gives
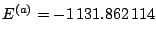 MeV and
MeV and
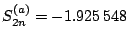 MeV.
Here, the last significant digit corresponds to 0.001keV, which is the
accuracy required to stop the iterations when we solve the HFB
equations for any given value of
MeV.
Here, the last significant digit corresponds to 0.001keV, which is the
accuracy required to stop the iterations when we solve the HFB
equations for any given value of
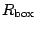 .
The fluctuations around the average values
result from the individual continuum states entering into
the cut-off window with increasing
.
The fluctuations around the average values
result from the individual continuum states entering into
the cut-off window with increasing
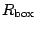 .
We see that for relatively small boxes (
.
We see that for relatively small boxes (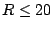 fm) the
two-neutron separation energy is an order of magnitude more
stable than the total binding energy of the nucleus.
For
fm) the
two-neutron separation energy is an order of magnitude more
stable than the total binding energy of the nucleus.
For 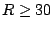 fm, the two quantities reach their asymptotic
values with a random dispersion of about 0.5 keV.
The value of
fm, the two quantities reach their asymptotic
values with a random dispersion of about 0.5 keV.
The value of
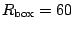 fm is obviously unnecessarily
large but it represents a good test of the stability of the
integration procedure. From these results we conclude that
the solution of the HFB equations with the box boundary conditions
and the energy cut-off is precise up to about 1keV.
fm is obviously unnecessarily
large but it represents a good test of the stability of the
integration procedure. From these results we conclude that
the solution of the HFB equations with the box boundary conditions
and the energy cut-off is precise up to about 1keV.
A typical asymptotic behaviour of the particle and pairing densities
for neutrons
is shown in Fig. 4 for two different choices of the boundary condition.
The impact of the boundary conditions only shows
up within about 5fm near the box edge. It is
small enough to have no significant effect on the calculated
observables.
Figure 4:
Neutron particle and pairing densities in 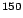 Sn
for Dirichlet (solid line) and Neumann (dashed line)
boundary conditions. The inset represents the same
quantities on a linear scale, in that case the impact of
the boundary condition cannot be seen.
Sn
for Dirichlet (solid line) and Neumann (dashed line)
boundary conditions. The inset represents the same
quantities on a linear scale, in that case the impact of
the boundary condition cannot be seen.
|
|
Neutron particle and pairing densities for different sizes of the box
are shown in Fig. 5.
The box radius of 10fm is obviously too small and it has only been
included
to show the effect of a very small box on the densities.
For
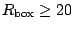 fm, no differences can be seen in the linear
scale. An interesting fact is that despite the cut that
has been applied for the pairing field at
fm, no differences can be seen in the linear
scale. An interesting fact is that despite the cut that
has been applied for the pairing field at
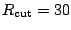 fm,
see Sec. 5.3,
no consequences can be observed on the densities in the asymptotic region.
fm,
see Sec. 5.3,
no consequences can be observed on the densities in the asymptotic region.
Figure:
Neutron particle (left) and pairing (right) densities for different box sizes.
In the insets the dashed lines correspond to
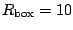 fm
while the solid lines correspond to the other
values of
fm
while the solid lines correspond to the other
values of
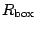 that cannot be separated in the linear scale.
that cannot be separated in the linear scale.
|
|



Next: Regularization of the pairing
Up: Examples
Previous: Examples
Jacek Dobaczewski
2005-01-23
![]() Sn (
Sn (![]() and
and ![]() )
using the effective force SLy4
)
using the effective force SLy4
![]() .
This
nucleus is an interesting example since it has a rather small
neutron Fermi energy (
.
This
nucleus is an interesting example since it has a rather small
neutron Fermi energy (
![]() MeV).
Small neutron separation energy allows us to discuss
possible effects of the integration box size as well as
the choice of the boundary condition.
If not explicitly stated otherwise, in all calculations the
integration step is
MeV).
Small neutron separation energy allows us to discuss
possible effects of the integration box size as well as
the choice of the boundary condition.
If not explicitly stated otherwise, in all calculations the
integration step is ![]() fm
for the box size of
fm
for the box size of
![]() fm, i.e., the number of
integration points is 150+1.
The global properties
of the nucleus for Dirichlet or Neumann boundary
condition are shown in table 5.
fm, i.e., the number of
integration points is 150+1.
The global properties
of the nucleus for Dirichlet or Neumann boundary
condition are shown in table 5.
![]() with different values of
with different values of ![]() and indeed different asymptotic
bahaviour. The single particle neutron states in the vicinity
of the Fermi energy are shown in table 6. It is
gratifying to observe that despite the fact that the quasiparticle
states are a little bit influenced by the change of the boundary
conditions, the canonical states remain unchanged.
and indeed different asymptotic
bahaviour. The single particle neutron states in the vicinity
of the Fermi energy are shown in table 6. It is
gratifying to observe that despite the fact that the quasiparticle
states are a little bit influenced by the change of the boundary
conditions, the canonical states remain unchanged.
![]() , which has to by consistent with the
mass of the nucleus.
The convergence of the kinetic, pairing,
and total energies are shown in the left part of Fig. 2.
Between
, which has to by consistent with the
mass of the nucleus.
The convergence of the kinetic, pairing,
and total energies are shown in the left part of Fig. 2.
Between
![]() and 37 the total energy
difference is 1.3keV.
The changes in the kinetic and pairing energies are a little
bit bigger (7keV and 6keV, respectively); since these
quantities are not at their extrema,
they react more rapidly to a small change of the wave function.
and 37 the total energy
difference is 1.3keV.
The changes in the kinetic and pairing energies are a little
bit bigger (7keV and 6keV, respectively); since these
quantities are not at their extrema,
they react more rapidly to a small change of the wave function.
![$ \begin{matrix}
\includegraphics*[scale=0.51,bb=37 52 392 497]{fig1.ps} \ \ &
\includegraphics*[scale=0.51,bb=22 52 404 497]{fig1bis.ps} \\
\end{matrix}$](img296.png)
![\includegraphics[scale=0.55,bb=74 53 489 345, clip]{fig2.ps}](img299.png)
![\includegraphics[scale=0.52,bb=67 55 488 326, clip]{fig5.ps}](img308.png)
![]() fm, no differences can be seen in the linear
scale. An interesting fact is that despite the cut that
has been applied for the pairing field at
fm, no differences can be seen in the linear
scale. An interesting fact is that despite the cut that
has been applied for the pairing field at
![]() fm,
see Sec. 5.3,
no consequences can be observed on the densities in the asymptotic region.
fm,
see Sec. 5.3,
no consequences can be observed on the densities in the asymptotic region.
![$ \begin{matrix}
\includegraphics*[scale=0.42,bb=36 55 487 328]{fig6.ps} &
\ \includegraphics*[scale=0.42,bb=36 55 487 328]{fig7.ps} \\
\end{matrix}$](img311.png)