


Next: The Hartree-Fock-Bogolyubov energy
Up: The Skyrme Hartree-Fock-Bogolyubov equations
Previous: Local densities
In the code HFBRAD the solutions are restricted
to have a spherical symmetry and do not mix proton
and neutron states. In this situation the
wave functions have the good quantum numbers
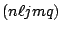 (
(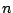 is a good quantum number since the spectrum is discretized
inside a spherical box)
and all the solutions inside an
is a good quantum number since the spectrum is discretized
inside a spherical box)
and all the solutions inside an
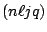 -block are
degenerated. Furthermore, the radial part of the wave functions
can be chosen to be real. Thus we use the ansatz
-block are
degenerated. Furthermore, the radial part of the wave functions
can be chosen to be real. Thus we use the ansatz
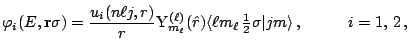 |
(9) |
for the wave functions. The local densities can be written
using the radial functions (omitting the isospin quantum number)
For the kinetic densities we have
Finally the spin current vector densities have only one non vanishing
component given by



Next: The Hartree-Fock-Bogolyubov energy
Up: The Skyrme Hartree-Fock-Bogolyubov equations
Previous: Local densities
Jacek Dobaczewski
2005-01-23
![]() (
(![]() is a good quantum number since the spectrum is discretized
inside a spherical box)
and all the solutions inside an
is a good quantum number since the spectrum is discretized
inside a spherical box)
and all the solutions inside an
![]() -block are
degenerated. Furthermore, the radial part of the wave functions
can be chosen to be real. Thus we use the ansatz
-block are
degenerated. Furthermore, the radial part of the wave functions
can be chosen to be real. Thus we use the ansatz
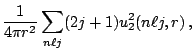
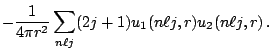
![$\displaystyle \displaystyle
\sum_{n\ell j}\frac{2j+1}{4\pi r^2}
\left[
\left(u_...
...l j,r)}{r}\right)^2
+\frac{\ell(\ell+1)}{r^2}u_2^2(n\ell j,r)
\right]\,,
\hfill$](img64.png)
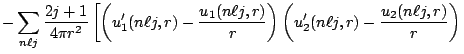
![$\displaystyle \hfill\displaystyle +\left.\frac{\ell(\ell+1)}{r^2}u_1(n\ell j,r)u_2(n\ell j,r)
\right]\,.$](img67.png)
![$\displaystyle \displaystyle \frac{1}{4\pi r^3}\sum_{n\ell j}(2j+1)
\left[j(j+1)-\ell(\ell+1)-\frac{3}{4}\right]u_2^2(n\ell j,r)\,,\hfill$](img69.png)
![$\displaystyle \displaystyle -\frac{1}{4\pi r^3}\sum_{n\ell j}(2j+1)
\left[j(j+1)-\ell(\ell+1)-\frac{3}{4}\right]u_1(n\ell j,r)u_2(n\ell j,r)\,.$](img71.png)