


Next: The Hartree-Fock-Bogolyubov mean fields
Up: The Skyrme Hartree-Fock-Bogolyubov equations
Previous: Spherical symmetry
In the Skyrme-HFB approximation, the total energy
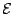 of a
nucleus is given as a sum of kinetic, Skyrme, pairing and Coulomb
terms:
of a
nucleus is given as a sum of kinetic, Skyrme, pairing and Coulomb
terms:
The derivation of the energy is explained in detail in several
articles (see Refs. [3,11] for the HF energy
and [5] for the HFB case). The expression of the Skyrme
force is given in section 3.
In equation (17),
the kinetic energy of both neutrons and protons is given by
isoscalar kinetic density. The neutron and proton
masses being approximated by their average value, and one has
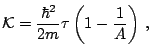 |
(17) |
where the factor in parentheses takes into account the
direct part of the center-of-mass correction [12].
Since we only consider even-even nuclei, the Skyrme part of the
energy functional is time even, it can be written as a sum of
isoscalar (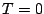 ) and isovector (
) and isovector (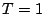 ) parts (see e.g.
Ref. [13])
or as a sum on isoscalar, neutrons and protons densities,
) parts (see e.g.
Ref. [13])
or as a sum on isoscalar, neutrons and protons densities,
Index 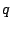 stands for neutrons and protons while the absence
of index indicates the total (isoscalar) density.
Using the same notations for the densities, the pairing energy density reads
stands for neutrons and protons while the absence
of index indicates the total (isoscalar) density.
Using the same notations for the densities, the pairing energy density reads
![$\displaystyle \mathcal{E}_{\mathrm{pair}}=\displaystyle
\sum_q \left\{ \frac{t_...
...tilde\tau_q+\frac{1}{4}\left(\nabla\tilde\rho_q\right)^2
\right]\right.\ \ \ \ $](img89.png) |
|
|
|
![$\displaystyle \displaystyle \hfill\left.+\left[\frac{t_2'}{8}(1+x_2')+
\frac{1}...
...right]\tilde J_q^2
+\frac{t_3'}{24}(1-x_3')\rho^{\gamma'}\tilde\rho_q^2\right\}$](img90.png) |
|
|
(19) |
In this last expression we have added a prime to the parameters
of the interaction. Although the derivation of the general
Skyrme energy density functional is based on a unique force,
its effective nature justifies the use of different
sets of parameters in the particle-hole and particle-particle
channels. The prime indices anticipates this possibility
which is discussed in section 3.
The energy density defined in (17) involves
a Coulomb term for protons. This term contains a direct
part which can be expressed using the charge density and
leads to a local field after variation of the energy and an
exchange part which would lead to a non local potential. Both
parts deserve a special discussion.
The direct part of the
Coulomb energy depends on the charge density
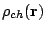 and reads
and reads
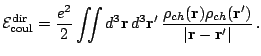 |
(20) |
We use the point proton density to simplify this expression,
i.e. the charge density is replaced by the proton density
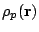 . Nevertheless, the proton form factor is taken
into account when we calculate the charge radius of the nucleus
(see eq. (57)).
The exchange part of the Coulomb energy leads to a non local term
and is treated with the Slater approximation. This approximation
means that we keep only the first term of the density matrix
expansion in the local density approximation [14]
. Nevertheless, the proton form factor is taken
into account when we calculate the charge radius of the nucleus
(see eq. (57)).
The exchange part of the Coulomb energy leads to a non local term
and is treated with the Slater approximation. This approximation
means that we keep only the first term of the density matrix
expansion in the local density approximation [14]
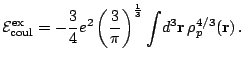 |
(21) |
The error introduced by this approximation
has been estimated by studying the next order
term [15] or more recently by comparison with the
exact treatment of the Coulomb energy [16].
The Slater approximation seems to have little consequence on the nuclei
bulk properties although some significant effects can be expected
on the position of the proton drip-line and the Coulomb displacement
energy of single particle levels.
Finally, the Coulomb contributions to the pairing energy and fields
are not included in the HFBRAD code.



Next: The Hartree-Fock-Bogolyubov mean fields
Up: The Skyrme Hartree-Fock-Bogolyubov equations
Previous: Spherical symmetry
Jacek Dobaczewski
2005-01-23
![]() of a
nucleus is given as a sum of kinetic, Skyrme, pairing and Coulomb
terms:
of a
nucleus is given as a sum of kinetic, Skyrme, pairing and Coulomb
terms:
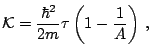
![$\displaystyle \mathcal{E}_{\mathrm{pair}}=\displaystyle
\sum_q \left\{ \frac{t_...
...tilde\tau_q+\frac{1}{4}\left(\nabla\tilde\rho_q\right)^2
\right]\right.\ \ \ \ $](img89.png)
![$\displaystyle \displaystyle \hfill\left.+\left[\frac{t_2'}{8}(1+x_2')+
\frac{1}...
...right]\tilde J_q^2
+\frac{t_3'}{24}(1-x_3')\rho^{\gamma'}\tilde\rho_q^2\right\}$](img90.png)
![]() and reads
and reads