


Next: The effective Skyrme force
Up: The Skyrme Hartree-Fock-Bogolyubov equations
Previous: Asymptotic properties of the
Pairing correlations and divergence of the energy
The use of a zero range interaction in the particle-particle channel
leads to the energy divergence problem [9,19] related to the
fact that the short-range behaviour of the abnormal density is
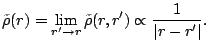 |
(37) |
The other abnormal densities diverge as well, but along that
the pairing correlations also
induce the divergence of the kinetic density 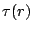 .
One simple way to overcome the divergence of the energy is
to introduce a cut-off energy
.
One simple way to overcome the divergence of the energy is
to introduce a cut-off energy
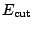 in the summations of all the densities
in the summations of all the densities
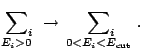 |
(38) |
This cut-off somehow simulates the finite range of the interaction in
the pairing channel. It therefore constitutes
an additional parameter of the interaction
and must be adjusted along with the other quantities which define
the pairing interaction, see e.g. Ref. [18].
A more elegant way to prevent the divergence was recently
proposed in Refs. [9,19]. It is based on the
subtractions of the divergent part of the abnormal density.
In its present implementation in the code HFBRAD,
this method can only be applied if the pairing force
does not contains non-local terms (i.e. gradient
terms). In that case, the pairing energy depends only
on
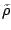 (and possibly on
(and possibly on 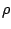 but not on
but not on
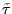 or
or 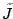 ), i.e.,
), i.e.,
![$\displaystyle \mathcal{E}_{\mathrm{pair}}=\sum_q \left[\frac{t_0'}{4}(1-x_0')+\...
...{24}(1-x_3')\rho^{\gamma'}\right] \tilde\rho_q^2=\sum_q g[\rho]\tilde\rho_q^2 ,$](img154.png) |
(39) |
and the pairing potential depends linearly on
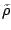 ,
,
![$\displaystyle \tilde U_q=2 g[\rho]\tilde\rho_q\,.$](img155.png) |
(40) |
The regularized pairing field can then be written as
![$\displaystyle \tilde U^{\mathrm{reg}}_q=2 g[\rho]\tilde\rho_q^{\mathrm{reg}} \equiv2 g_{\mathrm{eff}}[\rho]\tilde\rho_q\,.$](img156.png) |
(41) |
Calculation of the various densities is performed by summing up
the quasiparticle contributions up to a maximum energy
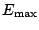 , but because
of the regularization, this maximum energy has not the meaning
of a cut-off energy
, but because
of the regularization, this maximum energy has not the meaning
of a cut-off energy
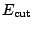 .
.
It can be shown [19]
that when we evaluate the total energy of the system,
the pairing energy must be defined as
![$\displaystyle \mathcal{E}_{\mathrm{pair}}=\sum_q g_{\mathrm{eff}}[\rho]\tilde\rho_q^2\,.$](img158.png) |
(42) |
With this definition, the kinetic and pairing energies both diverge
but the sum, and indeed the total energy, does not [19].
If the pairing energy density involves kinetic or gradient
terms (like it was implemented for the Skyrme interaction SkP [5]),
the regularization would
require the subtraction of higher order terms. This possibility
in not implemented in the present version of the code.
Finally, let us note that
relations (21)-(26) in Ref. [19] imply that the
variation of quantities 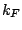 and
and 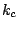 with respect
to the densities should be included in the mean fields.
This contribution is supposed to be small
and is not taken into account in the code. On the other hand,
for density-dependent pairing interaction, the variation with
respect to the explicit density dependence is taken into account
in the code, and gives a contribution to the energy of the order
of a few keV.
with respect
to the densities should be included in the mean fields.
This contribution is supposed to be small
and is not taken into account in the code. On the other hand,
for density-dependent pairing interaction, the variation with
respect to the explicit density dependence is taken into account
in the code, and gives a contribution to the energy of the order
of a few keV.



Next: The effective Skyrme force
Up: The Skyrme Hartree-Fock-Bogolyubov equations
Previous: Asymptotic properties of the
Jacek Dobaczewski
2005-01-23
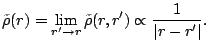
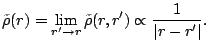
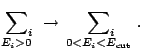
![]() (and possibly on
(and possibly on ![]() but not on
but not on
![]() or
or ![]() ), i.e.,
), i.e.,
![$\displaystyle \mathcal{E}_{\mathrm{pair}}=\sum_q \left[\frac{t_0'}{4}(1-x_0')+\...
...{24}(1-x_3')\rho^{\gamma'}\right] \tilde\rho_q^2=\sum_q g[\rho]\tilde\rho_q^2 ,$](img154.png)
![$\displaystyle \mathcal{E}_{\mathrm{pair}}=\sum_q g_{\mathrm{eff}}[\rho]\tilde\rho_q^2\,.$](img158.png)