


Next: Coulomb Interaction
Up: Skyrme Hartree-Fock-Bogoliubov Method
Previous: Calculations of Matrix Elements
Calculation of Local Densities
After diagonalizing the HFB equation (37),
local densities are calculated as
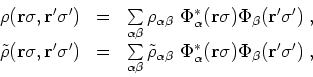 |
(46) |
where
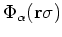 denotes the HO or THO basis wave functions,
and the matrix elements of mean-field and pairing density matrices read
denotes the HO or THO basis wave functions,
and the matrix elements of mean-field and pairing density matrices read
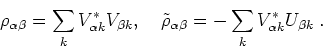 |
(47) |
The HFB calculations for zero-range pairing interaction give
divergent energies when increasing the number of quasiparticle states
in the sums of Eq. (47) (see discussion in
Ref. [3]). Therefore, they invariably require a truncation
of quasiparticle basis by defining a cut-off quasiparticle energy
and including all quasiparticle states only up to
this value.
The choice of an appropriate cut-off procedure has been discussed
in [2]. After each iteration, performed with a given
Fermi energy 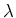 , one calculates an equivalent spectrum
, one calculates an equivalent spectrum
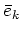 and pairing gaps
and pairing gaps
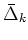 :
:
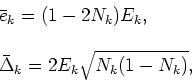 |
(48) |
where 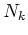 denotes the norm (23) of the lower HFB wave
function. Using this spectrum and pairing gaps, the Fermi energy is
readjusted to obtain the correct value of particle number, and this
new value is used in the next HFB iteration.
denotes the norm (23) of the lower HFB wave
function. Using this spectrum and pairing gaps, the Fermi energy is
readjusted to obtain the correct value of particle number, and this
new value is used in the next HFB iteration.
Due to the similarity between the equivalent spectrum
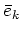 and the single-particle energies, one can take
into account only those quasiparticle states for which
and the single-particle energies, one can take
into account only those quasiparticle states for which
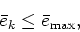 |
(49) |
where
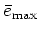
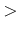 0 is a parameter defining the amount of
the positive-energy phase space taken into account. Since all
hole-like quasiparticle states,
0 is a parameter defining the amount of
the positive-energy phase space taken into account. Since all
hole-like quasiparticle states, 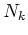
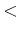 1/2, have negative values of
1/2, have negative values of 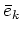 , condition (49) guarantees that they are all
taken into account. In this way, a global cut-off prescription is
defined which fulfills the requirement of taking into account the
positive-energy phase space as well as all quasiparticle states
up to the highest hole-like quasiparticle energy. In the code, a
default value of
, condition (49) guarantees that they are all
taken into account. In this way, a global cut-off prescription is
defined which fulfills the requirement of taking into account the
positive-energy phase space as well as all quasiparticle states
up to the highest hole-like quasiparticle energy. In the code, a
default value of
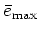 =60 MeV is used.
=60 MeV is used.



Next: Coulomb Interaction
Up: Skyrme Hartree-Fock-Bogoliubov Method
Previous: Calculations of Matrix Elements
Jacek Dobaczewski
2004-06-25
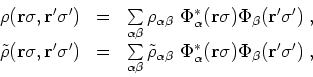
![]() , one calculates an equivalent spectrum
, one calculates an equivalent spectrum
![]() and pairing gaps
and pairing gaps
![]() :
:
![]() and the single-particle energies, one can take
into account only those quasiparticle states for which
and the single-particle energies, one can take
into account only those quasiparticle states for which