


Next: Calculation of Local Densities
Up: Skyrme Hartree-Fock-Bogoliubov Method
Previous: HFB Diagonalization in Configurational
Calculations of Matrix Elements
As discussed in Sect. 3.2, local densities (25) and
average fields, (17) and (18), are calculated in the
coordinate space. Therefore, calculation of matrix elements
(38) amounts to calculating appropriate spatial integrals in
the cylindrical coordinates 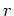 and
and 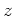 . In practice, the integration
is carried out by using the Gauss quadratures [31] for 22
Gauss-Hermite points in the
. In practice, the integration
is carried out by using the Gauss quadratures [31] for 22
Gauss-Hermite points in the 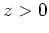 direction and 22 Gauss-Laguerre points
in the
direction and 22 Gauss-Laguerre points
in the 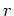 direction. This gives a sufficient
accuracy for calculations up to
direction. This gives a sufficient
accuracy for calculations up to 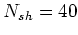 .
.
In the case of the HO basis functions, the integration is performed
by using the Gauss integration points, 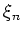 and
and 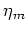 , for which
the local densities and fields have to be calculated at the
mesh points of
, for which
the local densities and fields have to be calculated at the
mesh points of 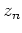 =
=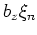 and
and 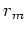 =
=
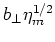 . As an
example, consider the following diagonal matrix element of the
potential
. As an
example, consider the following diagonal matrix element of the
potential 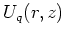 (18),
(18),
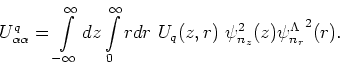 |
(39) |
Inserting here the HO functions
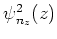 and
and
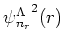 (29), and changing the integration
variables to dimensionless variables
(29), and changing the integration
variables to dimensionless variables 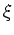 and
and 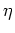 , the above
matrix element reads
, the above
matrix element reads
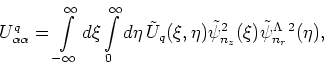 |
(40) |
where
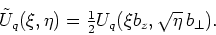 |
(41) |
Here, the Gauss integration quadratures can be directly applied, because
the HO wave functions contain appropriate exponential profile functions.
The situation is a little bit more complicated in the case of the THO basis
states where, before calculating, one has to change variables with
respect to the LST functions  . For example, let us
consider the same matrix elements (39) but in THO representation:
. For example, let us
consider the same matrix elements (39) but in THO representation:
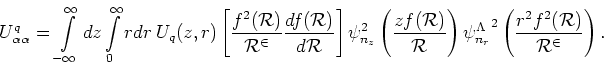 |
(42) |
Introducing new dimensionless variables
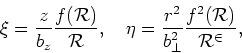 |
(43) |
for which we have
![\begin{displaymath}
d\xi~d\eta=\frac{2}{b_{z}b_{\bot}^{2}}\left[ \frac{f^{2}(\ma...
...{R}^{2}}\frac{df(\mathcal{R})}{d\mathcal{R}}\right] r d r~ dz,
\end{displaymath}](img158.png) |
(44) |
the matrix elements have the form of integrals, which are exactly identical
to those in the HO basis (40), after changing the function
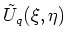 to
to
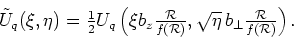 |
(45) |
The calculation of matrix elements corresponding to derivative terms in
the Hamiltonian (17) can be performed in an analogous way,
after the derivatives of the Jacobian,
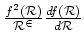 , are taken
into account.
, are taken
into account.



Next: Calculation of Local Densities
Up: Skyrme Hartree-Fock-Bogoliubov Method
Previous: HFB Diagonalization in Configurational
Jacek Dobaczewski
2004-06-25
![]() and
and ![]() . In practice, the integration
is carried out by using the Gauss quadratures [31] for 22
Gauss-Hermite points in the
. In practice, the integration
is carried out by using the Gauss quadratures [31] for 22
Gauss-Hermite points in the ![]() direction and 22 Gauss-Laguerre points
in the
direction and 22 Gauss-Laguerre points
in the ![]() direction. This gives a sufficient
accuracy for calculations up to
direction. This gives a sufficient
accuracy for calculations up to ![]() .
.
![]() and
and ![]() , for which
the local densities and fields have to be calculated at the
mesh points of
, for which
the local densities and fields have to be calculated at the
mesh points of ![]() =
=![]() and
and ![]() =
=
![]() . As an
example, consider the following diagonal matrix element of the
potential
. As an
example, consider the following diagonal matrix element of the
potential ![]() (18),
(18),
![]() . For example, let us
consider the same matrix elements (39) but in THO representation:
. For example, let us
consider the same matrix elements (39) but in THO representation:
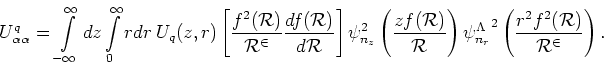
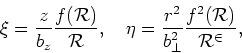
![\begin{displaymath}
d\xi~d\eta=\frac{2}{b_{z}b_{\bot}^{2}}\left[ \frac{f^{2}(\ma...
...{R}^{2}}\frac{df(\mathcal{R})}{d\mathcal{R}}\right] r d r~ dz,
\end{displaymath}](img158.png)