


Next: Symmetry-covariant energy density
Up: Symmetries
Previous: Symmetries
Symmetry-invariant energy density
Based on the derivation after separation of symmetries, which we
introduced above, it is clear that we can proceed by separating
densities into irreducible representations of all required symmetries
and then building the energy density by taking scalar products
separately in each of the representations. Such a construction gives
a symmetry-invariant energy density,
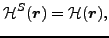 |
(80) |
where
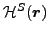 denotes the energy density calculated
for a many-body state transformed by the symmetry operator
denotes the energy density calculated
for a many-body state transformed by the symmetry operator 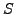 .
This guarantees the invariance of the EDF and total energy (1) with
respect to all considered symmetries. Such a strategy would also
allow for using arbitrary, unrelated to one another coupling
constants in each of the irreducible representations.
.
This guarantees the invariance of the EDF and total energy (1) with
respect to all considered symmetries. Such a strategy would also
allow for using arbitrary, unrelated to one another coupling
constants in each of the irreducible representations.
However, in practical applications, such a strategy was never up to
now fully implemented--neither at N LO, for which the present
study is the first attempt in the literature, nor at NLO, which
corresponds to the standard Skyrme functionals (see Sec. 3.1
below). Only the time reversal and isospin symmetries were up to now
treated in this way, and below we are going to follow the same path.
LO, for which the present
study is the first attempt in the literature, nor at NLO, which
corresponds to the standard Skyrme functionals (see Sec. 3.1
below). Only the time reversal and isospin symmetries were up to now
treated in this way, and below we are going to follow the same path.
For the time reversal, all local densities discussed in
Sec. 2.3 are either time-even or time-odd. Indeed, this
simply follows from the facts [25] that
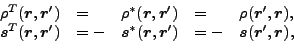 |
(81) |
which give the time-even and time-odd parts in Eqs. (65)
and (66) as
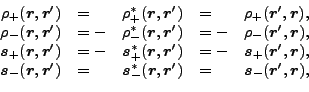 |
(82) |
i.e.,
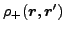 and
and
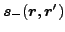 are real symmetric functions and
are real symmetric functions and
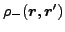 and
and
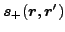 are imaginary antisymmetric functions.
Moreover, the relative momentum operator
are imaginary antisymmetric functions.
Moreover, the relative momentum operator 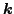 (6),
which defines derivative operators
(6),
which defines derivative operators 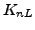 , is imaginary and
antisymmetric with respect to exchanging variables
, is imaginary and
antisymmetric with respect to exchanging variables 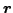 and
and
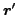 . Altogether, it is easy to see that
. Altogether, it is easy to see that 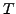 -parities
of primary densities
-parities
of primary densities
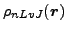 (23)
are equal to
(23)
are equal to
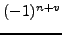 , see Eq. (25) and columns denoted by
, see Eq. (25) and columns denoted by 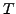 in
Tables 3 and 4. Similarly,
in
Tables 3 and 4. Similarly, 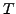 -parities
of secondary densities
-parities
of secondary densities
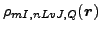 (24)
are also equal to
(24)
are also equal to
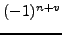 . Construction of the
. Construction of the 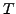 -invariant
energy density (80) can now be realized by
multiplying densities that have identical
-invariant
energy density (80) can now be realized by
multiplying densities that have identical 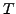 -parities.
-parities.



Next: Symmetry-covariant energy density
Up: Symmetries
Previous: Symmetries
Jacek Dobaczewski
2008-10-06
![]() LO, for which the present
study is the first attempt in the literature, nor at NLO, which
corresponds to the standard Skyrme functionals (see Sec. 3.1
below). Only the time reversal and isospin symmetries were up to now
treated in this way, and below we are going to follow the same path.
LO, for which the present
study is the first attempt in the literature, nor at NLO, which
corresponds to the standard Skyrme functionals (see Sec. 3.1
below). Only the time reversal and isospin symmetries were up to now
treated in this way, and below we are going to follow the same path.