A fascinating phenomenon of increased radial sizes of nuclei far from
stability [41,42,43,44] was very intensely
studied in recent years. In extreme situations, when nuclei consist
of about thrice more neutrons than protons, the outer weakly bound
neutrons may form halos of particle densities extending to rather
large distances. For example, the flag-ship nucleus 11Li
exhibiting this kind of structure has the measured [45]
root-mean-square (rms) radius of
![]() =3.27(24)fm, while in 9Li
one has
=3.27(24)fm, while in 9Li
one has
![]() =2.43(2)fm. Supposing that in 11Li the
size of the ``core'' subsystem of 9 particles is the same as that
of 9Li, one obtains the rms radius of the
two-neutron subsystem equal to
=2.43(2)fm. Supposing that in 11Li the
size of the ``core'' subsystem of 9 particles is the same as that
of 9Li, one obtains the rms radius of the
two-neutron subsystem equal to
![]() =5.67fm. Therefore, the outer
two-neutrons occupy a volume that has the size similar to that of
208Pb, which is a nucleus with about 20 times more particles!
=5.67fm. Therefore, the outer
two-neutrons occupy a volume that has the size similar to that of
208Pb, which is a nucleus with about 20 times more particles!
Sizes of several light neutron-rich nuclei were recently measured via the total interaction cross sections, see Refs. [46,47,48]. Although such measurements rely on a number of theoretical assumptions pertaining to the reaction mechanism, the increase of size of nuclei near the drip lines seems to be fairly well established. The question of increased sizes of medium heavy and heavy neutron-rich nuclei could be so far addressed only in theoretical calculations within mean-field models. The decisive role played by pairing correlations in establishing asymptotic density distributions has been recognized since a long time [49,50], and several calculations based on the Bogoliubov approach were already performed, both in the non-relativistic [51,52,53] and in the relativistic [54,55,56,57] framework.
The neutron rms radius constitutes only an indicative general measure of the neutron density distribution. In fact, three different physical properties of the density distribution can be singled out that strongly influence the rms radius, namely, (i) the global size of the nucleus, (ii) the surface diffuseness, and (iii) the rate of decrease of density in the asymptotic region. These three properties are almost directly related to (i) the number of nucleons, (ii) the surface tension or surface interaction terms, and (iii) the particle binding energy or the Fermi energy, respectively. The halo phenomena are obviously related to properties of particle distributions in the asymptotic region. One should keep in mind, however, that we cannot expect nuclear halos to correspond to what one might infer from the every-day-life meaning of the term. The nuclear density distributions always decrease when the distance from the center of nucleus increases, and by the halo we can only mean an unusually slow rate of such a decrease.
In order to disentangle the three effects mentioned above, one has to
use a sufficiently rich model of the neutron distribution. For
example, the density distributions obtained by filling with particles
the harmonic-oscillator (HO) potential up to a given principal HO
number cannot serve this purpose, because they are determined by a
single parameter, the HO frequency
![]() .
Therefore,
neither the surface diffuseness nor the asymptotic decrease rate can
be properly described, even if
.
Therefore,
neither the surface diffuseness nor the asymptotic decrease rate can
be properly described, even if
![]() is adjusted to
reproduce the overall size of the nucleus. Similarly, the Fermi (or
the Woods-Saxon) type of shape,
is adjusted to
reproduce the overall size of the nucleus. Similarly, the Fermi (or
the Woods-Saxon) type of shape,
Density distributions obtained within microscopic self-consistent
approaches are obviously able to independently model all three
physical effects described above. Here, the quantitative reproduction
of the nuclear size, surface diffuseness, and asymptotic decrease
rate depends on properties of the underlying interactions, while the
density distributions may in principle assume unrestricted forms. By
employing the classic Helm model distributions
[60,61,62], a
method to analyze microscopic distributions was recently devised
[53]. A comparison of Fourier transforms
(form factors) of the Helm and microscopic densities allows to define
the diffraction radius R0 and the surface thickness ![]() from
the positions of the first zero and first maximum of the form factor,
respectively. These characteristics of the density are entirely
independent of the asymptotic decrease rate, and hence they define a
suitable Helm rms reference radius,
from
the positions of the first zero and first maximum of the form factor,
respectively. These characteristics of the density are entirely
independent of the asymptotic decrease rate, and hence they define a
suitable Helm rms reference radius,
 |
In Ref. [53] it was shown that in the mean-field
description of medium heavy and heavy nuclei,
the neutron halos appear gradually when the neutron numbers increase
beyond the neutron magic numbers. The halos of different sizes
can be obtained by changing the parameterizations of nuclear
effective interactions, and in particular those of the pairing
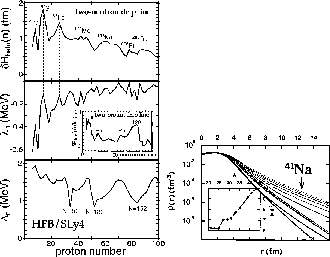
force [63]. Results of calculations presented
in the left panel of Fig. 3 indicate that the sizes of halos at the two-neutron
drip line are of the order of 1fm throughout the mass table.
Fluctuations that are observed in function of the mass number are
correlated with the values of the neutron Fermi energy ![]() .
However, no correlation is observed with the positions of the
Fermi energy with respect to the low-
.
However, no correlation is observed with the positions of the
Fermi energy with respect to the low-![]() (s and p) single-particle
orbitals. This latter fact reflects the so-called pairing anti-halo effect
[64].
(s and p) single-particle
orbitals. This latter fact reflects the so-called pairing anti-halo effect
[64].
Indeed, the pairing correlations strongly modify the asymptotic
properties of single-particle densities. In the extreme
single-particle picture, the single-particle ![]() =0 wave functions
behave asymptotically as
=0 wave functions
behave asymptotically as ![]()
![]()
![]() ,
with
the decrease rate of
,
with
the decrease rate of ![]() =
=
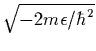 given by
the single-particle energy
given by
the single-particle energy ![]() .
Therefore, with
.
Therefore, with
![]()
![]() 0, these wave functions become infinitely
flat, and the corresponding rms radii, and the halo sizes, become
infinite. Nothing of the sort is observed in the
Hartree-Fock-Bogoliubov (HFB) calculations,
because here the lower components of the quasiparticle wave
functions vanish exponentially with the decrease rate of
0, these wave functions become infinitely
flat, and the corresponding rms radii, and the halo sizes, become
infinite. Nothing of the sort is observed in the
Hartree-Fock-Bogoliubov (HFB) calculations,
because here the lower components of the quasiparticle wave
functions vanish exponentially with the decrease rate of
![]() =
=
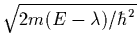 given by the quasiparticle
energy E [49,50]. Since the paring correlations do
not vanish at drip lines, the nonzero values of E prevent
given by the quasiparticle
energy E [49,50]. Since the paring correlations do
not vanish at drip lines, the nonzero values of E prevent ![]() from vanishing, even in the limit of zero binding given by
from vanishing, even in the limit of zero binding given by
![]() =0. As the result, one of the conditions generally thought
to be a prerequisite for the halo structures [65], i.e., the
presence of the low-
=0. As the result, one of the conditions generally thought
to be a prerequisite for the halo structures [65], i.e., the
presence of the low-![]() orbitals, does not apply to paired
even-N systems. On the other hand, this condition does apply to
odd-N systems, because the blocked HFB states correspond to the
quasiparticle wave functions that vanish with the decrease rate of
orbitals, does not apply to paired
even-N systems. On the other hand, this condition does apply to
odd-N systems, because the blocked HFB states correspond to the
quasiparticle wave functions that vanish with the decrease rate of
![]() =
=
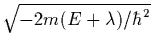 ,
which goes to zero at the
one-neutron drip line given by
,
which goes to zero at the
one-neutron drip line given by ![]() =0.
=0.
The fact that the neutron densities of even-N systems decrease with a non-zero rate when approaching the drip line is well born out in all self-consistent Bogoliubov calculations. An example obtained within the relativistic mean field (RMF) approach [54] is shown in the right panel of Fig. 3. Results for all bound even-N sodium isotopes were calculated in space coordinates, and the resulting matter density distributions clearly show a common non-zero decrease rate when approaching the neutron drip line, which simply illustrates the pairing anti-halo effect. This is especially strongly accentuated in the RMF+HB method which gives a cluster of nearly degenerate states close to the Fermi surface [54], which results in strong pairing correlations near the neutron drip line. Exactly the same situation occurs in the zirconium isotopes studied in Ref. [55].