Within the MF approximation, the isospin symmetry breaking has two
sources. The spontaneous breaking of isospin associated with the MF
approximation itself [36,26,29]
is, in this theory, intertwined with the explicit symmetry breaking
due to the Coulomb interaction. The essence of our
method [28,29] is to retain
the explicit isospin mixing. It is achieved by rediagonalizing the
total effective nuclear Hamiltonian
![]() in good-isospin
basis. The basis is generated by using the
projection-after-variation technique, that is, by acting with
the standard one-dimensional isospin-projection operator on
the MF product state
in good-isospin
basis. The basis is generated by using the
projection-after-variation technique, that is, by acting with
the standard one-dimensional isospin-projection operator on
the MF product state
![]() :
:
The total nuclear Hamiltonian consists of the kinetic
energy ![]() , the Skyrme interaction
, the Skyrme interaction
![]() and the
Coulomb interaction
and the
Coulomb interaction
![]() that breaks isospin:
that breaks isospin:
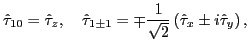 |
(9) |
The Coulomb interaction is the only source of
the isospin symmetry violation in our model. Charge symmetry breaking
components of the strong interaction and the isovector kinetic
energy (which is quenched as compared to its isoscalar counterpart
by a factor
![]() due to very small
mass difference
due to very small
mass difference ![]() between the neutron and the proton relative to
mean nucleonic mass
between the neutron and the proton relative to
mean nucleonic mass ![]() ) are not taken into account.
Hence, the isoscalar part of the total
Hamiltonian reads
) are not taken into account.
Hence, the isoscalar part of the total
Hamiltonian reads
![]() . Its matrix elements can be cast into
one-dimensional integrals:
. Its matrix elements can be cast into
one-dimensional integrals:
Calculation of matrix elements of the isovector (7) and isotensor (8)
components of the Coulomb interaction is slightly more complicated. It appears, however,
that these matrix elements can also be reduced to one-dimensional integrals
over the Euler angle ![]() :
:
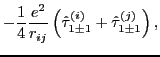 |
(14) | ||
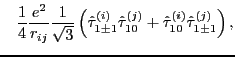 |
(15) | ||
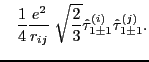 |
(16) |
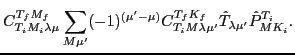 |
(18) |
The cornerstone of the isospin projection scheme described above is a
calculation of the Hamiltonian and norm kernels and subsequent
one-dimensional
integration over the Euler angle ![]() . The integrals are calculated
numerically using the Gauss-Legandre quadrature, which is very well suited for this problem provided that the calculated kernels
are non-singular.
. The integrals are calculated
numerically using the Gauss-Legandre quadrature, which is very well suited for this problem provided that the calculated kernels
are non-singular.