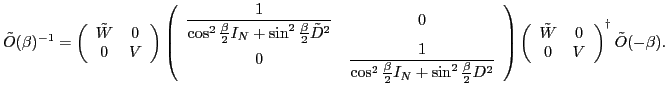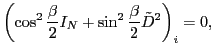Next: Isospin structure of the
Up: Theory
Previous: Isospin projection formalism
A prerequisite for the calculation of the integrals in Eqs. (2),
(10), and (13)
is the isospin rotation of the Slater determinant.
To this end, one has to perform an independent rotation of
s.p. neutron,
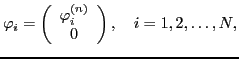 |
(19) |
and proton,
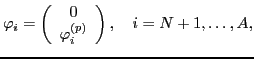 |
(20) |
HF wave functions. The use of the two-dimensional (spinor) representation of isospin constitutes
a natural formalism
for the isospin projection technique.
In this representation, the upper (neutron, 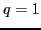 )
and lower (proton,
)
and lower (proton, 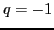 ) components of the isospin-rotated states are given by:
) components of the isospin-rotated states are given by:
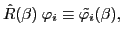 |
(21) |
where
To calculate the kernel
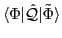 of an arbitrary
operator
of an arbitrary
operator
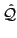 between two non-orthogonal Slater determinants,
we apply the generalized Wick's theorem,
see, e.g., Ref. [39]. In particular, the norm kernel
can be written in a compact form:
between two non-orthogonal Slater determinants,
we apply the generalized Wick's theorem,
see, e.g., Ref. [39]. In particular, the norm kernel
can be written in a compact form:
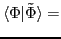 Det Det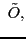 |
(24) |
where the overlap matrix is:
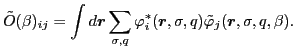 |
(25) |
To calculate kernels appearing in the projection formalism, one needs to
invert the
overlap matrix
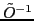 . This can cause serious problems due to the presence of singularities [22,40].
The regularization of kernel singularities is a difficult problem [23]. Thus far, a
regularization scheme has been worked out only for a very specific class
of functionals (or effective density-dependent
interactions) solely involving integer powers of local densities [23].
Unfortunately, almost all commonly used Skyrme and Gogny parameterizations, except for SIII [41],
involve fractional powers of the density. The appearance of singularities prevents us
from using the local Slater approximation for the
Coulomb exchange. In the present work we treat it exactly using the method of the Gaussian
decomposition of the Coulomb interaction, as described in
Refs. [42,43].
. This can cause serious problems due to the presence of singularities [22,40].
The regularization of kernel singularities is a difficult problem [23]. Thus far, a
regularization scheme has been worked out only for a very specific class
of functionals (or effective density-dependent
interactions) solely involving integer powers of local densities [23].
Unfortunately, almost all commonly used Skyrme and Gogny parameterizations, except for SIII [41],
involve fractional powers of the density. The appearance of singularities prevents us
from using the local Slater approximation for the
Coulomb exchange. In the present work we treat it exactly using the method of the Gaussian
decomposition of the Coulomb interaction, as described in
Refs. [42,43].
Compared to the particle number
or the angular momentum projection schemes, isospin projection is a relatively simple procedure. In particular,
the dependence of the inverse matrix
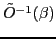 on the isorotation angle
on the isorotation angle 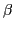 can be determined
analytically and this enables us to demonstrate that
the isospin projection is free from kernel singularities. To this end, we write
the overlap matrix (25)
in the form:
can be determined
analytically and this enables us to demonstrate that
the isospin projection is free from kernel singularities. To this end, we write
the overlap matrix (25)
in the form:
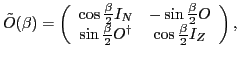 |
(26) |
where 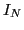 (
(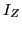 ) stands for the
) stands for the 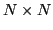 (
(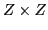 )
unit matrix, while
)
unit matrix, while
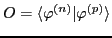 is the rectangular
is the rectangular 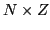 overlap matrix of the
neutron and proton s.p.
wave functions. Using the singular value
decomposition (SVD) technique, the matrix
overlap matrix of the
neutron and proton s.p.
wave functions. Using the singular value
decomposition (SVD) technique, the matrix 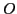 can be written as:
can be written as:
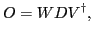 |
(27) |
where 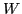 is an
is an 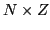 rectangular matrix having orthogonal columns
(
rectangular matrix having orthogonal columns
(
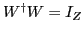 ),
),
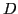 is a diagonal
is a diagonal 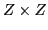 real and non-negative matrix
(
real and non-negative matrix
(
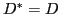 ), and
), and  is a
is a
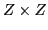 quadratic unitary matrix
(
quadratic unitary matrix
(
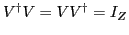 ). The SVD
decomposition (27) further implies that:
). The SVD
decomposition (27) further implies that:
 |
(28a) |
where
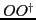 and
and
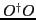 are matrices of
dimension
are matrices of
dimension 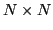 and
and 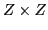 , respectively.
, respectively.
The SVD decomposition allows us to analytically diagonalize the overlap matrix
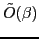 . Without loss of generality we assume
that
. Without loss of generality we assume
that 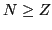 . Hence, the product
. Hence, the product
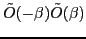 can be written as:
can be written as:
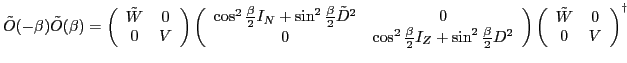 |
(29) |
where
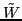 of dimension
of dimension 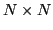 is a unitary matrix
composed of columns
is a unitary matrix
composed of columns 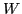 :
:
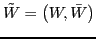 where where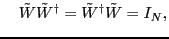 |
(30) |
and 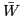 is the unitary complement.
is the unitary complement.
The
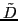 matrix, on the other hand, is the
matrix, on the other hand, is the
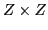 matrix
matrix 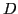 completed to the dimension
completed to the dimension
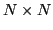 by zeros:
by zeros:
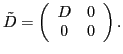 |
(31) |
Since the first and third matrices on the right hand side of Eq. (29)
are unitary and the second
matrix is diagonal, the inverse of the overlap matrix reads:
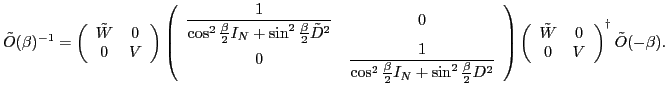 |
(32) |
This expression shows explicitly
that the inverse of the overlap matrix
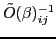 can be singular only if
can be singular only if
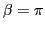 .
Indeed, in the case of
.
Indeed, in the case of
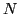 =
=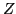 , the
, the 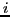 th denominator becomes zero,
th denominator becomes zero,
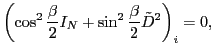 |
(33) |
only when
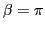 and the corresponding
singular value vanishes:
and the corresponding
singular value vanishes: 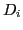 =0. In the case of
=0. In the case of 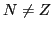 , the only difference
is that the matrix
, the only difference
is that the matrix
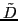 contains zeros by construction, see
Eq. (31). Fortunately, for the isospin projection, the singularity at
contains zeros by construction, see
Eq. (31). Fortunately, for the isospin projection, the singularity at
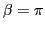 is compensated by the Jacobian
is compensated by the Jacobian
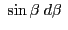 .
.



Next: Isospin structure of the
Up: Theory
Previous: Isospin projection formalism
Jacek Dobaczewski
2010-01-30
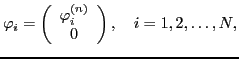
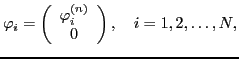
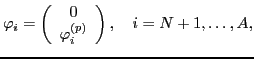
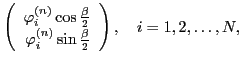
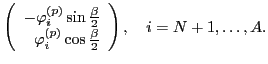
![]() of an arbitrary
operator
of an arbitrary
operator
![]() between two non-orthogonal Slater determinants,
we apply the generalized Wick's theorem,
see, e.g., Ref. [39]. In particular, the norm kernel
can be written in a compact form:
between two non-orthogonal Slater determinants,
we apply the generalized Wick's theorem,
see, e.g., Ref. [39]. In particular, the norm kernel
can be written in a compact form:
![]() . This can cause serious problems due to the presence of singularities [22,40].
The regularization of kernel singularities is a difficult problem [23]. Thus far, a
regularization scheme has been worked out only for a very specific class
of functionals (or effective density-dependent
interactions) solely involving integer powers of local densities [23].
Unfortunately, almost all commonly used Skyrme and Gogny parameterizations, except for SIII [41],
involve fractional powers of the density. The appearance of singularities prevents us
from using the local Slater approximation for the
Coulomb exchange. In the present work we treat it exactly using the method of the Gaussian
decomposition of the Coulomb interaction, as described in
Refs. [42,43].
. This can cause serious problems due to the presence of singularities [22,40].
The regularization of kernel singularities is a difficult problem [23]. Thus far, a
regularization scheme has been worked out only for a very specific class
of functionals (or effective density-dependent
interactions) solely involving integer powers of local densities [23].
Unfortunately, almost all commonly used Skyrme and Gogny parameterizations, except for SIII [41],
involve fractional powers of the density. The appearance of singularities prevents us
from using the local Slater approximation for the
Coulomb exchange. In the present work we treat it exactly using the method of the Gaussian
decomposition of the Coulomb interaction, as described in
Refs. [42,43].
![]() on the isorotation angle
on the isorotation angle ![]() can be determined
analytically and this enables us to demonstrate that
the isospin projection is free from kernel singularities. To this end, we write
the overlap matrix (25)
in the form:
can be determined
analytically and this enables us to demonstrate that
the isospin projection is free from kernel singularities. To this end, we write
the overlap matrix (25)
in the form:
![]() . Without loss of generality we assume
that
. Without loss of generality we assume
that ![]() . Hence, the product
. Hence, the product
![]() can be written as:
can be written as:
![]() matrix, on the other hand, is the
matrix, on the other hand, is the
![]() matrix
matrix ![]() completed to the dimension
completed to the dimension
![]() by zeros:
by zeros: