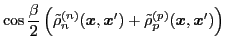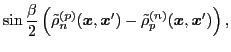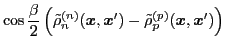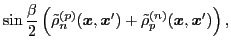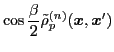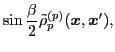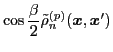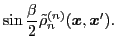Next: Hamiltonian kernel
Up: Theory
Previous: Inverse of the overlap
To calculate the transition density matrix and determine
its isotopic structure
it is convenient to introduce auxiliary ket-states
defined as:
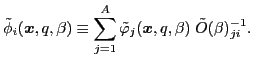 |
(34) |
where the space-spin coordinates are abbreviated as
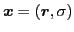 .
This allows for rewriting the transition
density matrix into a diagonal form:
.
This allows for rewriting the transition
density matrix into a diagonal form:
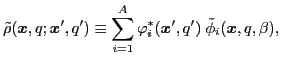 |
(35) |
where the summation runs over a set of s.p. states, in full analogy with
the HF particle density matrix. To alleviate the notation, in what follows
we do not indicate the dependence of the transition density
matrices on the isorotation angle 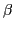 .
.
An arbitrary matrix in the isospace can be decomposed in terms of the isospin Pauli
matrices. In particular, the
transition density matrix
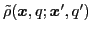 can be expressed as:
can be expressed as:
where
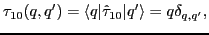 |
|
|
(37) |
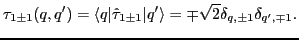 |
|
|
(38) |
The isoscalar
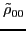 and isovector
and isovector
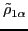 transition density matrices are calculated by contracting
transition density matrices are calculated by contracting
 :
:
The use of the two-dimensional spinor notation is convenient for
analytical derivations. However, from the numerical-programming perspective it is
better to present expressions in a one-dimensional
form, because it allows us to exploit the separability of proton and neutron
wave functions and densities - a common feature of essentially all the
existing HF codes including the HFODD solver used in this work.
To write the isoscalar and isovector densities in the one-dimensional form
we introduce
two sets of neutron-like (
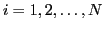 ) wave functions:
) wave functions:
and two sets of proton-like (
 )
wave functions:
)
wave functions:
Again, the dependence of these states on the isorotation angle 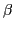 is not explicitly indicated.
Using these wave functions, we define two neutron-like
densities:
is not explicitly indicated.
Using these wave functions, we define two neutron-like
densities:
and two proton-like densities:
In these definitions, subscripts indicate whether the density is neutron- or
proton-like and superscripts indicate whether the
summation indices in Eqs. (40)-(43) run over neutron or proton states.
The densities
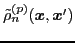 and
and
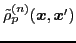 can be associated, respectively, with the raising and lowering components of the
analog spin [44,45].
can be associated, respectively, with the raising and lowering components of the
analog spin [44,45].
The isoscalar and isovector densities (39)
can now be expressed by using
the auxiliary densities (44)-(47), and they read



Next: Hamiltonian kernel
Up: Theory
Previous: Inverse of the overlap
Jacek Dobaczewski
2010-01-30
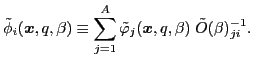
![]() can be expressed as:
can be expressed as:
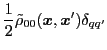
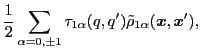
![]() ) wave functions:
) wave functions: