Non-Linear
The non-linear ![]() model Gel60,Wei67 is built to
describe pseudoscalar mesons of which we know that: 1
model Gel60,Wei67 is built to
describe pseudoscalar mesons of which we know that: 1![]() they
exist, 2
they
exist, 2![]() their scalar partners don't, and 3
their scalar partners don't, and 3![]() they obey
the chiral symmetry of SU(2)
they obey
the chiral symmetry of SU(2)![]() SU(2). The first two facts are
experimental ones, and the third one comes from the lower level
(quark) theory.
SU(2). The first two facts are
experimental ones, and the third one comes from the lower level
(quark) theory.
The SU(2)![]() SU(2) group is isomorphic to the O(4) group - the
orthogonal group in four dimensions Gil74. Therefore,
the meson fields in question can be described by four real fields
SU(2) group is isomorphic to the O(4) group - the
orthogonal group in four dimensions Gil74. Therefore,
the meson fields in question can be described by four real fields
![]() ,
, ![]() =1,2,3,4, and all we need is a model for the Lagrangian density.
The non-linear
=1,2,3,4, and all we need is a model for the Lagrangian density.
The non-linear ![]() model makes the following postulate:
model makes the following postulate:
 |
Let us now consider the classical ground state corresponding to
Lagrangian density (32). The lowest energy corresponds to
particles at rest,
![]() =0, and resting at a lowest
point of the potential energy (34). Now we have a problem
- which one of the lowest points to choose, because any one such that
=0, and resting at a lowest
point of the potential energy (34). Now we have a problem
- which one of the lowest points to choose, because any one such that
![]() =
=![]() is as good as any other one.
However, the classical fields
is as good as any other one.
However, the classical fields ![]() at space-time point
at space-time point ![]() must have definite values, i.e., they spontaneously pick
one of the solutions
must have definite values, i.e., they spontaneously pick
one of the solutions ![]() out of the infinitely-many
existing ones. Once one of the solutions is picked, the O(4) symmetry
is broken, because the ground-state field is not any more invariant
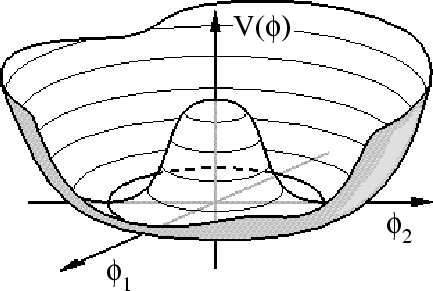
with respect to all O(4) transformations. Using the graphical
representation of the ``Mexican hat'', Fig. 4, one can say
that the system rolls down from the top of the hat, and picks one of
the points within the brim.
out of the infinitely-many
existing ones. Once one of the solutions is picked, the O(4) symmetry
is broken, because the ground-state field is not any more invariant
with respect to all O(4) transformations. Using the graphical
representation of the ``Mexican hat'', Fig. 4, one can say
that the system rolls down from the top of the hat, and picks one of
the points within the brim.
It is now clear that fields ![]() do not constitute the best
variables to look at the problem, because the physics in the radial and
transversal directions is different. Before proceeding any
further, let us introduce variables
do not constitute the best
variables to look at the problem, because the physics in the radial and
transversal directions is different. Before proceeding any
further, let us introduce variables ![]() and
and ![]() that
separately describe these two directions, namely,
that
separately describe these two directions, namely,
We disregard now the part of the Lagrangian density depending on ![]() .
Indeed, the initial potential (33) has been postulated
without any deep reason, and a detailed form of it is, in fact, totally
unknown - it comes from the quark level that we did not at all solved.
Any potential that confines the field
.
Indeed, the initial potential (33) has been postulated
without any deep reason, and a detailed form of it is, in fact, totally
unknown - it comes from the quark level that we did not at all solved.
Any potential that confines the field ![]() to values close to
to values close to
![]() is good enough. This field must remain in its ground state,
because any excitations of it would bring too much energy into a meson,
and again, meson's internal structure remains unresolved.
is good enough. This field must remain in its ground state,
because any excitations of it would bring too much energy into a meson,
and again, meson's internal structure remains unresolved.