Nucleon-Nucleon Interaction

Let us discuss in some more detail the interaction between nucleons. In the past there has been a tremendous experimental effort devoted to scattering protons on protons and neutrons on protons. Since the neutron target is not available, the neutron-neutron scattering was inferred mostly from the scattering of protons on deuterons. All this effort lead to a large database of cross-sections and phase shifts that provide the most extensive information on the binary interactions on nucleons. There have also been numerous attempts to model the interaction between nucleons by different kinds of potentials. Here we limit the discussion to the Argonne v$_{18}$ potential Wir95, and refer the reader to this paper for references to other existing approaches.

The Argonne v$_{18}$ NN interaction consists of the electromagnetic $V^{\mbox{\scriptsize {EM}}}$, one-pion-exchange $V^\pi(NN)$, and intermediate and short-range phenomenological $V^{\mbox{\scriptsize {R}}}(NN)$ parts, i.e.,

$$V(NN) = V^{\mbox{\scriptsize {EM}}}(NN) + V^\pi(NN) + V^{\mbox{\scriptsize {R}}}(NN) .$$ (47)

The electromagnetic part contains not only the standard Coulomb interaction between protons, but also various other terms like the two-photon Coulomb terms, vacuum polarization terms, and magnetic-moment interactions. The OPE potential results directly from the nucleon-pion Lagrangian discussed in Sec. 2.5.3, and has the following explicit form (here shown for the $p$-$p$ interaction):

$$V^\pi(pp) = f_{pp}^2{\textstyle{\frac{1}{3}}}m_\pi \left[Y(... ...}_i\cdot\mbox{{\boldmath {$\sigma$}}}_j + T(r)S_{ij}\right] ,$$ (48)

where

$$Y(r) = \frac{e^{-m_\pi r}}{r}\left(1-e^{-cr^2}\right) ,$$ (49)

$$T(r) = \left(1+\frac{3}{m_\pi r}+\frac{3}{(m_\pi r)^2}\right) \frac{e^{-m_\pi r}}{r}\left(1-e^{-cr^2}\right)^2 ,$$ (50)

and $S_{ij}$= $3(\mbox{{\boldmath {$\sigma$}}}_i\cdot\mbox{{\boldmath {$r$}}})(\mbox{{\boldmat... ...r$}}})/r^2 -\mbox{{\boldmath {$\sigma$}}}_i\cdot\mbox{{\boldmath {$\sigma$}}}_j$ is the tensor operator which depends on the Pauli matrices of the $i$th and $j$th interacting particles. The standard OPE terms have been supplemented with the cut-off factors $\big(1-e^{-cr^2}\big)$ that kill these terms at distances smaller than $r_c$=$1/\sqrt{c}$, i.e., below $r_c$=0.69fm for the used value of $c$=1.21fm$^{-2}$. There, the remaining terms come into play:

$$V^{\mbox{\scriptsize {R}}} = V^{\mbox{\scriptsize {c}}} + V^... ... {ls}}} L\cdot S + V^{\mbox{\scriptsize {ls2}}} (L\cdot S)^2 ,$$ (51)

where the i=c, l2, t, ls, and ls2 terms read

$$V^{\mbox{\scriptsize {i}}}(r) = I^{\mbox{\scriptsize {i}}}T^... ... {i}}} (m_\pi r)^2\right] \left(1+e^{(r-r_0)/a}\right)^{-1} ,$$ (52)

and $I^{\mbox{\scriptsize {i}}}$, $P^{\mbox{\scriptsize {i}}}$, $Q^{\mbox{\scriptsize {i}}}$, and $R^{\mbox{\scriptsize {i}}}$ are parameters fitted to the scattering data. These terms are cut off at large distances, i.e., above $r_0$=0.5fm, with the transition region of the width of $a$=0.2fm.

The Argonne v$_{18}$ potential adopts the point of view that at large distances the NN interaction is governed by the OPE effects, while the short-range part is treated fully phenomenologically. In this respect, there is a perfect analogy between the strong force acting between nucleons, as modelled by Argonne v$_{18}$, and the electromagnetic force acting between neutral non-polar molecules, modelled by the Lennard-Jones potential.

Nucleons are colorless objects, i.e., when looked upon from the outside; no net color charge is visible. The same is true for neutral non-polar molecules that contain equal amounts of positive and negative electromagnetic charges distributed with no net shift, and hence they have no net charge or dipole moment. However, when two molecules approach one another, the charges become polarized, and each molecule acquires a non-zero dipole moment. Then the leading-order interaction energy between molecules equals $V(\mbox{{\boldmath {$r$}}})$= $-2\mbox{{\boldmath {$E$}}}(\mbox{{\boldmath {$r$}}})\cdot\mbox{{\boldmath {$d$}}}(\mbox{{\boldmath {$r$}}})$, where $\mbox{{\boldmath {$E$}}}(\mbox{{\boldmath {$r$}}})$ is the average electric field felt by one of the molecules when the second one is located at $\mbox{{\boldmath {$r$}}}$, and $\mbox{{\boldmath {$d$}}}(\mbox{{\boldmath {$r$}}})$ is its dipole moment. Assuming that the induced dipole moment $\mbox{{\boldmath {$d$}}}(\mbox{{\boldmath {$r$}}})$ depends linearly on the electric field, and knowing that the electric field created by a dipole decreases as $1/r^3$, we obtain immediately that $V(\mbox{{\boldmath {$r$}}})$$\sim$$-1/r^6$, which gives the well-known Van der Waals potential. At intermediate and small distances, polarization effects become stronger, and higher induced multipole moments begin to be active, however, we can model these effects by a phenomenological term that is equal to the square of the Van der Waals term. Together, one obtains the Lennard-Jones potential,

$$V_{\mbox{\scriptsize {LJ}}}(r) = 4 E_{p,0}\left[\left(\frac{... ...}{r}\right)^{12} -\left(\frac{\sigma}{r}\right)^{6} \right] ,$$ (53)

where $E_{p,0}$ and $\sigma$ are parameters fitted to data.

Figure 5: The $^1$S$_0$-channel $n$-$n$ potential in megaelectronovolts (MeV), as function of the distance in femtometers (fm) (inner axes) compared with the O$_2$-O$_2$ molecular potential in millielectronovolts (meV), as function of the distance in nanometers (nm) (outer axes).

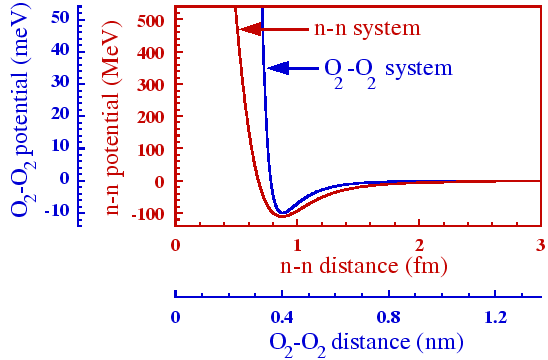In Fig. 5 we show a comparison of the $n$-$n$ Argonne v$_{18}$ potential in the $^1$S$_0$ channel, with the Lennard-Jones potential between two O$_2$ molecules ($E_{p,0}$=10meV and $\sigma$=0.358nm). The Argonne v$_{18}$ potential has been calculated by using the av18pw.f FORTRAN subroutine Wir95, available at http://www.phy.anl.gov/theory/research/av18/av18pot.f. Both potentials are drawn in the same Figure with two abscissas (the lower one for O$_2$-O$_2$, the upper one for $n$-$n$) and two ordinates (the left one for O$_2$-O$_2$, the right one for $n$-$n$). Scales an the abscissas were fixed so as to put the minima of potentials at the same point, and differ by a factor of about 0.5$\times$10$^6$, while scales on the ordinates differ by the factor of 10$^{10}$.

Despite the tremendous differences in scales, both potentials are qualitatively very similar. Amazingly, it is the electromagnetic molecule-molecule potential that it stiffer at the minimum than the neutron-neutron ``strong'' potential. In this respect, it is fully justified to put the word ``strong'' into quotation marks - this potential is not strong at all! Both potentials exhibit a very strong repulsion at short distances - the so-called hard core (the O$_2$-O$_2$ repulsion is stronger!). At large distances, there appears a weak attraction (the $n$-$n$ attraction vanishes more slowly - despite the exponential form of the OPE potential). Neither of the potentials is strong enough to bind the constituents into a composite object.

The analogy between the ``strong'' NN force and the electromagnetic molecule-molecule force is extremely instructive. First of all, we can demystify the OPE potential in the sense that the exchange of real particles (pions) is, in fact, not its essential element. The OPE potential is a remnant of our tool (quantum field theory) that we used to derive it, but on a deeper level it is an effect of the color force between color-polarized composite particles. After all, nobody wants to interpret the dipole-dipole inter-molecular O$_2$-O$_2$ force by an exchange of a ``particle''. This force can be understood in terms of a more fundamental interaction - the Coulomb force. Second, although the asymptotic, large-distance, leading-order behaviour of both potentials can fairly easily be derived, at intermediate and small distances the interaction becomes very complicated. This is not a reflection of complications on the level of fundamental forces (color or electromagnetic), but a reflection of the complicated polarization effects that take place when composite objects are put close to one another. Moreover, these polarization effects have per se quantum character, because the fermionic constituents do not like being put close to one another - the Pauli exclusion principle creates additional polarization and repulsion effects. And third, it is obvious that at small distances there must appear effects that are of a three-body character. Namely, when three O$_2$ molecules approach each other (e.g., in liquid oxygen), the basic assumption that they polarize one another only in pairs does not hold. There are certainly polarization effects that depend on explicit positions of the three of them. Similarly, when three nucleons approach each other within the nucleus, their quark-gluon magma becomes polarized in a fairly complicated way, which on the level of potential energy (total-interaction energy) reveals additional terms depending on the three positions simultaneously; this gives the three-body NNN force.