


Next: Minute No. 3, the
Up: Quantum Field Theory in
Previous: Minute No. 1, the
Minute No. 2, the Quantum Mechanics
Quantum systems Mes71 are described by the wave function
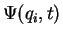 (complex function of coordinates
(complex function of coordinates 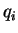 and time
and time 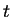 ),
and by the Hamilton operator
),
and by the Hamilton operator 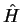 that can be obtained
from the classical Hamiltonian by a procedure called quantization.
We define operators that correspond to each classical object,
e.g., the classical coordinates and momenta are quantized as,
that can be obtained
from the classical Hamiltonian by a procedure called quantization.
We define operators that correspond to each classical object,
e.g., the classical coordinates and momenta are quantized as,
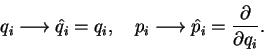 |
(7) |
Then, the Hamilton operator is, more or less, obtained by
inserting these operators into the classical Hamiltonian, i.e.,
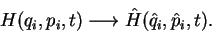 |
(8) |
This is not an exact science, because the function of operators
cannot be uniquely defined for a given function of variables;
one has to also define the order in which the operators act.
Well, in fact the quantization provides us only with general rules
on how to start the quantum mechanics based on our knowledge of the
classical mechanics. One can also subscribe to the point of view
that we must axiomatically define the quantum system by specifying
its Hamilton operator. Once this is done, the time evolution
of the system (of its wave function) is given by the Schrödinger equation,
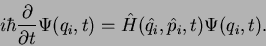 |
(9) |
This leads to a set coupled differential equations that can be, in
principle, solved once the initial conditions 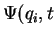 =0) are
known. One thus obtains the complete past and future history of the
system
=0) are
known. One thus obtains the complete past and future history of the
system 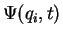 . The rest is just a technicality
;) of how to solve differential equations.
. The rest is just a technicality
;) of how to solve differential equations.
Quantum mechanics also adds a pivotal element to our understanding
of how our world works, namely, the probabilistic interpretation.
In classical mechanics, once our Euler-Lagrange equations give us
the set of coordinates 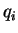 at time
at time 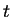 , the experiment performed
at time
, the experiment performed
at time 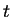 to find the system at point
to find the system at point 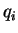 yields one possible
answer: the system is there. In quantum mechanics, the same experiment
yields the answer that the system is within volume
yields one possible
answer: the system is there. In quantum mechanics, the same experiment
yields the answer that the system is within volume 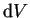 around
around
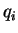 with probability
with probability
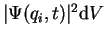 and the answer that
it is not there, with probability
and the answer that
it is not there, with probability
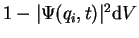 .
Hélas, it seems that the world is just like that, nothing is
certain any more. However, at least the probabilities of obtaining
given experimental answers can be rigorously calculated.
.
Hélas, it seems that the world is just like that, nothing is
certain any more. However, at least the probabilities of obtaining
given experimental answers can be rigorously calculated.



Next: Minute No. 3, the
Up: Quantum Field Theory in
Previous: Minute No. 1, the
Jacek Dobaczewski
2003-01-27
![]() (complex function of coordinates
(complex function of coordinates ![]() and time
and time ![]() ),
and by the Hamilton operator
),
and by the Hamilton operator ![]() that can be obtained
from the classical Hamiltonian by a procedure called quantization.
We define operators that correspond to each classical object,
e.g., the classical coordinates and momenta are quantized as,
that can be obtained
from the classical Hamiltonian by a procedure called quantization.
We define operators that correspond to each classical object,
e.g., the classical coordinates and momenta are quantized as,
![]() at time
at time ![]() , the experiment performed
at time
, the experiment performed
at time ![]() to find the system at point
to find the system at point ![]() yields one possible
answer: the system is there. In quantum mechanics, the same experiment
yields the answer that the system is within volume
yields one possible
answer: the system is there. In quantum mechanics, the same experiment
yields the answer that the system is within volume ![]() around
around
![]() with probability
with probability
![]() and the answer that
it is not there, with probability
and the answer that
it is not there, with probability
![]() .
Hélas, it seems that the world is just like that, nothing is
certain any more. However, at least the probabilities of obtaining
given experimental answers can be rigorously calculated.
.
Hélas, it seems that the world is just like that, nothing is
certain any more. However, at least the probabilities of obtaining
given experimental answers can be rigorously calculated.