


Next: Minute No. 2, the
Up: Quantum Field Theory in
Previous: Quantum Field Theory in
Minute No. 1, the Classical Mechanics
Classical systems Gol53 are described by defining two
elements: 1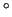 - the set of classical coordinates
- the set of classical coordinates 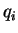 , which
are supposed to give a complete information about the state of the
system, and 2
, which
are supposed to give a complete information about the state of the
system, and 2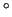 - the Lagrangian. The state depends on a
parameter called the classical absolute time
- the Lagrangian. The state depends on a
parameter called the classical absolute time 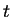 , and hence, coordinates
, and hence, coordinates
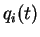 are functions of time. The Lagrangian,
are functions of time. The Lagrangian,
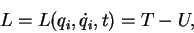 |
(1) |
is a function of coordinates 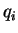 , velocities
, velocities 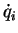 , and time
, and time
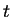 . According to the mechanistic point of view of the classical
mechanics, every system in our Universe, including the whole
Universe, is fully described by finding its coordinates and
Lagrangian. For most systems the Lagrangian is equal to a difference
of the kinetic energy
. According to the mechanistic point of view of the classical
mechanics, every system in our Universe, including the whole
Universe, is fully described by finding its coordinates and
Lagrangian. For most systems the Lagrangian is equal to a difference
of the kinetic energy 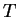 , depending only on velocities, and the
potential energy
, depending only on velocities, and the
potential energy 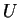 , depending only on coordinates [see the second
member of Eq. (1)].
, depending only on coordinates [see the second
member of Eq. (1)].
Once the system is defined as above, its properties can be derived from
simple principles. The time evolution of the system can be found
from the principle of extremal action 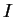 ,
,
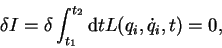 |
(2) |
which gives the Euler-Lagrange equations,
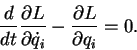 |
(3) |
This leads to a set coupled differential equations that can be, in
principle, solved once the initial conditions 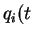 =0) and
=0) and
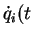 =0) are known. One thus obtains the complete past and
future history of the system
=0) are known. One thus obtains the complete past and
future history of the system 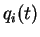 . The rest is
just a technicality ;) of how to solve differential equations. For
typical systems, the kinetic energy is a quadratic function of
velocities, for which the Euler-Lagrange equations are linear - and
can be solved fairly easily.
. The rest is
just a technicality ;) of how to solve differential equations. For
typical systems, the kinetic energy is a quadratic function of
velocities, for which the Euler-Lagrange equations are linear - and
can be solved fairly easily.
Although we do not really need it in classical mechanics, we shell
also introduce the formulation in terms of the Hamiltonian 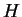 .
This gives us a bridge towards the quantum mechanics. Namely,
we define the classical momentum
.
This gives us a bridge towards the quantum mechanics. Namely,
we define the classical momentum 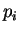 by
by
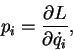 |
(4) |
and we transform the Lagrangian into the Hamiltonian,
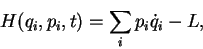 |
(5) |
as well as the Euler-Lagrange equations into the Hamilton equations,
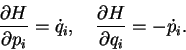 |
(6) |



Next: Minute No. 2, the
Up: Quantum Field Theory in
Previous: Quantum Field Theory in
Jacek Dobaczewski
2003-01-27
![]() - the set of classical coordinates
- the set of classical coordinates ![]() , which
are supposed to give a complete information about the state of the
system, and 2
, which
are supposed to give a complete information about the state of the
system, and 2![]() - the Lagrangian. The state depends on a
parameter called the classical absolute time
- the Lagrangian. The state depends on a
parameter called the classical absolute time ![]() , and hence, coordinates
, and hence, coordinates
![]() are functions of time. The Lagrangian,
are functions of time. The Lagrangian,
![]() ,
,
![]() .
This gives us a bridge towards the quantum mechanics. Namely,
we define the classical momentum
.
This gives us a bridge towards the quantum mechanics. Namely,
we define the classical momentum ![]() by
by