Quantum Chromodynamics (QCD)

It is remarkable that quantum chromodynamics Gra95that describes all phenomena related to strongly interacting particles, can be constructed in full analogy to the QED. The ``only'' difference is a more complicated gauge group, SU(3) instead of U(1). The complete QCD Lagrangian density reads

$${\cal L} = -{\textstyle{\frac{1}{4}}}F^\alpha_{\mu\nu}F_\alp... ...gA^\alpha_\mu t_\alpha]\psi_n - \sum_n m_n \bar{\psi}_n\psi_n$$ (21)

and it is composed almost of the same elements as the QED Lagrangian density in Eq. (16). The new object is the set of eight SU(3) 3$\times$3 matrices $t_\alpha$, numbered by the gluon-color index $\alpha$=1,...,8. They fulfill the SU(3) commutation relations

$$\left[t_\beta,t_\gamma\right]=iC^\alpha_{\beta\gamma}t_\alpha ,$$ (22)

where $C^\alpha_{\beta\gamma}$ are the SU(3) algebra structure constants Gil74. Again, every pair of gluon-color indices implies summation, e.g., over $\alpha$ in Eqs. (21) and (22).

Dirac four-spinors $\psi_n$ correspond to quark fields. Compared to the electron four-spinors $\psi_e$ discussed in Sec. 2.2, they are richer in two aspects. First, each of them appears in three variants, red, blue, and green. These colors are numbered by the quark-color index corresponding to the dimensions 3$\times$3 of the $t_\alpha$ matrices. Traditionally they are not explicitly shown in the Lagrangian density (22), so we should, in fact, think about $\psi_n$ as 12-component spinors. One should not be confused by the fact that there are three colors of quarks, and eight colors of gluons - in fact, here the "visual" representation simply breaks down, and the colors of gluons have nothing to do with red, blue, and green of quarks. In reality, quarks and gluons are numbered by the indices of the corresponding SU(3) representations: three-dimensional spinor representation for quarks, and eight-dimensional vector representation for gluons.

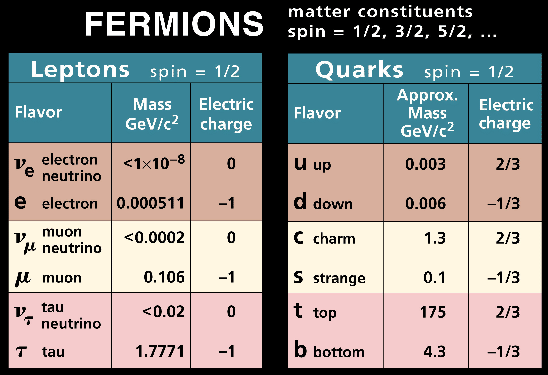
Second, there is not one, but six different quark fields, for $n$=1,...,6. These are called quark flavors, and are usually denoted by names: up, down, charm, strange, top, and bottom, see Fig. 1. For nuclear structure physics, essential rôle is played only by the up and down quarks that are constituents of neutrons and protons. So in most applications of the QCD to nuclear structure, we can limit the QCD Lagrangian density to two flavors only, $n$=1, 2.

Figure 1: Fermion building blocks for electroweak (left) and strong (right) interactions. From http://www.cpepweb.org/.

The first term in the QCD Lagrangian density (21) describes the free gluon fields defined by eight four-potentials $A^\alpha_\mu$. One can say that instead of one photon of the QED, that transmits the electromagnetic interaction, we have eight gluons that transmit the strong interaction, see Fig. 2.

Figure 2: Same as in Fig. (1) but for bosons. From http://www.cpepweb.org/.

The gluon field tensors $F^\alpha_{\mu\nu}$ are defined as

$$F^\alpha_{\mu\nu} = \partial_\mu A^\alpha_\nu - \partial_\... ...^\alpha_\mu + C^\alpha_{\beta\gamma}A^\beta_\mu A^\gamma_\nu.$$ (23)

Here comes the really big difference between the QED and QCD, namely, the gluon field tensors contain the third term in Eq. (23). As a result, gluons interact with one another - we can say that they are color-charged, while the photon has no charge. It is easy to see that the third term in Eq. (23) implies the charged gluons. Indeed, the Euler-Lagrange equations corresponding to the free gluon fields do produce the source terms when the Lagrangian density is varied with respect to the gluon fields. (In QED, the free-photon-field Lagrangian depends only on derivatives of the photon fields, and not on the photon fields themselves.)

The last term in (21) describes the six free quarks of masses $m_n$ at rest. This does not mean that isolated quarks can exist in Nature, be accelerated, and have their masses measured by their inertia with respect to acceleration. Each free quark obeys the same Dirac equation as the electron in QED. The Dirac equation is given by the last term and the $\partial_\mu$-term in Eq. (21). Quarks couple to gluons through the color currents,

$$J^\mu_\alpha = -ig \sum_n\bar{\psi}_n\gamma^\mu A^\alpha_\mu t_\alpha\psi_n .$$ (24)

We are going to discuss this aspect a few paragraphs below; here we only note that all quarks couple to gluons with the same value of the color charge $g$. We cannot give any numerical value to this parameter, because it depends on energy through the mechanism called renormalization, that we shall not discuss in the present course.

Consequences of the gluon charges are dramatic. Namely, the force carriers now exert the same force as the force they transmit. Moreover, sources of the electromagnetic field depend on currents (20) that involve a small parameter - the electron charge, while gluons constitute sources of the color field without any small parameter. Gluons are not only color-charged, but they also produce very strong color fields.

Let us now consider empty space. In a quantum field theory, we cannot just say that the ground state of the empty space is the state with no quanta - we have to solve the proper field equations, with proper boundary conditions, and determine what is the state of the field. Such a state may or may not contain quanta. In particular, whenever the space has a boundary, the ground state of the field does contain quanta - this fact is called the vacuum polarization effect.

In QED, this is a very well known, and experimentally verified effect. For example, two conducting parallel plates attract each other, even if they are not charged and placed in otherwise empty space (this is called the Casimir effect Plu86). One can understand this attraction very easily. Namely, the vacuum fluctuations of the electron field may create in an empty space virtual electron-positron pairs. These charged particles induce virtual polarization charges in the conducting plates (it means virtual photons are created, travel to plates, and reflect from them). Hence, the plates become virtually charged, and attract one another during a short time when the existence of the virtual charges, and virtual photons, is allowed by the Heisenberg principle. All in all, a net attractive force between plates appears.

In QED such effects are extremely weak, because the electron has a small charge and a non-zero rest mass. On the other hand, the QCD gluons are massless, and their strong interaction is not damped by a small parameter. As a result, the QCD vacuum polarization effect is extremely strong, and the empty space is not empty at all - it must contain a soup of spontaneously appearing, interacting, and disappearing gluons. Moreover, in the soup there also must be pairs of virtual quark-antiquark pairs that are also color-charged, and emit and absorb more virtual gluons. It turns out that the QCD ground state of an "empty" space is an extremely complicated object. At present, we do not have any glimpse of a possibility to find the vacuum wave function analytically. Some ideas of what happens are provided by the QCD lattice calculations, see e.g. Ref. Lei00, in which the gluon and quark fields are discretized on a four-dimensional lattice of space-time points, and the differential field equations are transformed into finite-difference equations solvable on a computer.

Figure 3: A snap-shot of the space color charge of the QCD vacuum, calculated on a space-time lattice. From http://hermes.physics.adelaide.edu.au/theory/staff/leinweber/ VisualQCD/QCDvacuum/welcome.html.

An example of such a result is shown in Fig. 3. It presents a frozen-frame image, however, the solution is obtained in space and time, and hence we know what happens at different times. One movie is worth thousands photos, so interested students are invited to visit the WEB site indicated in the Figure caption, to see the animation of the complete result. Only then one can appreciate the complexity of appearing structures, with blobs of color charge constantly appearing, disappearing and moving around. The QCD vacuum really resembles a soup of boiling gluons and quarks.

It is now obvious that one cannot expect other solutions of the QCD fields to be any simpler. In particular, solutions corresponding to isolated quarks simply do not exist. One can say that an isolated quark would create so many gluons around it that the complete wave function had not been normalizable. Solutions for quark-antiquark pairs, and for triples of quarks, do exist (we do exist after all - the triples of quarks are nucleons our bodies are built of), but are even more complicated to obtain, even within the QCD lattice calculations. There is no hope, neither there is any reason, to describe composite objects like mesons or nucleons directly from quarks and gluons. This is especially true when we want to use these composite objects to build the next-generation composite objects like nuclei.

Here we arrive at the leading idea of our physical description of the real world. Namely, a physicist always begins by isolating the most important degrees of freedom to describe a given system at a given energy and/or size scale. These degrees of freedom must be compatible with the ones that govern objects at a finer level of description, and must define the degrees of freedom useful at any coarser level of description. However, it is neither useful, nor sensible, nor fruitful, nor doable to overjump different levels. Why bother to derive the structure of a living cell from the unified QCD and electroweak Lagrangian? There are at least seven levels in between: nucleons are built of quarks, nuclei of nucleons, atoms of nuclei and electrons, molecules of atoms, amino acids of molecules, proteins of amino acids, and we did not arrive at a cell yet. Well, we shall not embark here on the philosophy of science; in the following we concentrate on describing how mesons and nucleons are built of quarks, and nuclei of nucleons.