


Next: Rotational and mirror symmetry
Up: Nonlocal and local densities
Previous: Nonlocal and local densities
Rotational symmetry SO(3)
If we assume that the density matrices
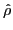 and
and
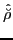 , Eqs. (1) and (2), are invariant under
the three-dimensional rotations forming the SO(3) group, it immediately follows from
Eqs. (5) and (6) that the densities of type
, Eqs. (1) and (2), are invariant under
the three-dimensional rotations forming the SO(3) group, it immediately follows from
Eqs. (5) and (6) that the densities of type
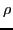 are the SO(3) scalars while the densities of type
are the SO(3) scalars while the densities of type
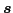 are the SO(3) vectors (note that the spin Pauli matrices are the SO(3)
vectors). Therefore, the nonlocal density of
type
are the SO(3) vectors (note that the spin Pauli matrices are the SO(3)
vectors). Therefore, the nonlocal density of
type 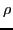 takes a form of Eq. (20):
takes a form of Eq. (20):
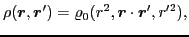 |
(26) |
while the nonlocal density of type 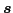 has a form of Eq. (21):
has a form of Eq. (21):
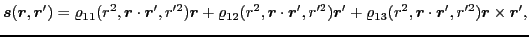 |
(27) |
where 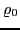 ,
,
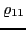 ,
,
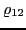 , and
, and
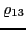 are
arbitrary scalar functions. All local differential densities
(11)-(18) can be calculated by differentiating
Eqs. (26) and (27), like it was done in
I. But to establish general forms of all local densities, it is
sufficient to realize that all of them are local isotropic fields
with definite transformation rules under SO(3) rotations. These
rules can be deduced from the definitions (9)-(18). We
see that the local densities
are
arbitrary scalar functions. All local differential densities
(11)-(18) can be calculated by differentiating
Eqs. (26) and (27), like it was done in
I. But to establish general forms of all local densities, it is
sufficient to realize that all of them are local isotropic fields
with definite transformation rules under SO(3) rotations. These
rules can be deduced from the definitions (9)-(18). We
see that the local densities
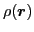 ,
,
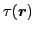 , and
, and
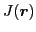 are scalar fields and all take the form of Eq. (23).
Similarly, the densities
are scalar fields and all take the form of Eq. (23).
Similarly, the densities
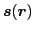 ,
,
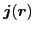 ,
,
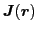 ,
,
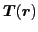 , and
, and
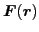 are
the SO(3) vectors; hence, are given by the form of Eq. (24). Finally, the
spin-current density
are
the SO(3) vectors; hence, are given by the form of Eq. (24). Finally, the
spin-current density
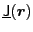 is the
traceless symmetric tensor of the form (25).
is the
traceless symmetric tensor of the form (25).



Next: Rotational and mirror symmetry
Up: Nonlocal and local densities
Previous: Nonlocal and local densities
Jacek Dobaczewski
2010-01-30
![]() and
and
![]() , Eqs. (1) and (2), are invariant under
the three-dimensional rotations forming the SO(3) group, it immediately follows from
Eqs. (5) and (6) that the densities of type
, Eqs. (1) and (2), are invariant under
the three-dimensional rotations forming the SO(3) group, it immediately follows from
Eqs. (5) and (6) that the densities of type
![]() are the SO(3) scalars while the densities of type
are the SO(3) scalars while the densities of type
![]() are the SO(3) vectors (note that the spin Pauli matrices are the SO(3)
vectors). Therefore, the nonlocal density of
type
are the SO(3) vectors (note that the spin Pauli matrices are the SO(3)
vectors). Therefore, the nonlocal density of
type ![]() takes a form of Eq. (20):
takes a form of Eq. (20):