

Next: Degenerate shell: Seniority model
Up: Limiting cases
Previous: Weak-pairing limit,
Strong-pairing limit, 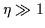
In this case, the expansion parameter is 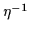 .
In the zero order, the wave function of an even system
with N=2n is the ground
state of
.
In the zero order, the wave function of an even system
with N=2n is the ground
state of
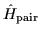 ;
i.e., it corresponds to the state
with the maximal quasispin
;
i.e., it corresponds to the state
with the maximal quasispin
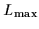 =
=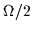 and
the third component of quasispin
L0=(2n-
and
the third component of quasispin
L0=(2n-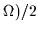 .
The binding energy is given by the seniority-model
expression (see Refs. [27,28] and Sec. 3.2),
.
The binding energy is given by the seniority-model
expression (see Refs. [27,28] and Sec. 3.2),
![\begin{displaymath}
B_{\eta\gg1}^{(0)}(N=2n) =-G \left[ L_{\mbox{\rm\scriptsize {max}}}(L_{\mbox{\rm\scriptsize {max}}}+1) -
L_0(L_0-1) \right].
\end{displaymath}](img76.gif) |
(26) |
In the quasispin formalism, the single-particle Hamiltonian is a combination
of a scalar and a vector operator (with respect to the quasispin group),
and this implies the
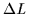 =0,
=0,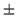 1 selection rule for its matrix elements.
The expectation value of
1 selection rule for its matrix elements.
The expectation value of
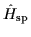 in the lowest
L=
in the lowest
L=
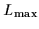 state is:
state is:
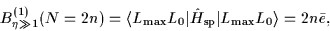 |
(27) |
where
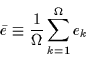 |
(28) |
is the average single-particle energy.
The second-order correction to the energy is given by
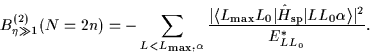 |
(29) |
In Eq. (28)
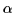 denotes all the remaining quantum numbers other than
L and L0,
and
E*LL0 is the unperturbed excitation energy of
denotes all the remaining quantum numbers other than
L and L0,
and
E*LL0 is the unperturbed excitation energy of
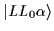 .
Since
.
Since
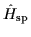 can only connect the
seniority-zero
ground state with the seniority-two, L=
can only connect the
seniority-zero
ground state with the seniority-two, L=
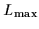 -1 states at
energy
-1 states at
energy
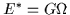 ,
Eq. (29) can be reduced to a simple form;
,
Eq. (29) can be reduced to a simple form;
By introducing the variance of single-particle levels,
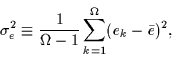 |
(31) |
one can derive a simple expression for the second-order correction:
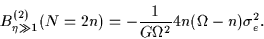 |
(32) |
That is, the first- and second-order corrections to the binding energy are
given by the first and second moments of the single-particle energy
distribution.
Note that for the degenerate j-shell, the second-order
correction is zero, as expected.
For odd particle numbers, N=2n+1, one should take
Lmax=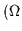 -1)/2 and L0=(2n+1-
-1)/2 and L0=(2n+1-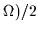 in Eq. (26). Assuming that the
odd particle occupies level n+1, this level is removed from the sum
of Eqs. (28) and (31),
i.e.,
one needs to consider the remaining
in Eq. (26). Assuming that the
odd particle occupies level n+1, this level is removed from the sum
of Eqs. (28) and (31),
i.e.,
one needs to consider the remaining 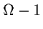 levels only:
levels only:
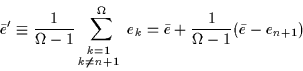 |
(33) |
and
The resulting corrections to the binding energies can be written as
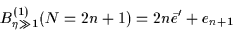 |
(35) |
and
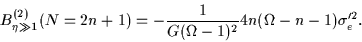 |
(36) |
The zero-order expressions for
 and
and
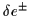 in the strong pairing limit are given in
Sec. 3.2.
By adding the zero- and first-order contributions to
the binding energy, one obtains
the strong-pairing-limit expressions for
in the strong pairing limit are given in
Sec. 3.2.
By adding the zero- and first-order contributions to
the binding energy, one obtains
the strong-pairing-limit expressions for
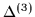 :
:
It can easily be shown that the first-order correction to 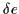 vanishes.
Consequently, the seniority-model expressions discussed below give a good
approximation to
the single-particle energy-splitting filters (7)
and (8).
vanishes.
Consequently, the seniority-model expressions discussed below give a good
approximation to
the single-particle energy-splitting filters (7)
and (8).


Next: Degenerate shell: Seniority model
Up: Limiting cases
Previous: Weak-pairing limit,
Jacek Dobaczewski
2000-03-09
![]() .
In the zero order, the wave function of an even system
with N=2n is the ground
state of
.
In the zero order, the wave function of an even system
with N=2n is the ground
state of
![]() ;
i.e., it corresponds to the state
with the maximal quasispin
;
i.e., it corresponds to the state
with the maximal quasispin
![]() =
=![]() and
the third component of quasispin
L0=(2n-
and
the third component of quasispin
L0=(2n-![]() .
The binding energy is given by the seniority-model
expression (see Refs. [27,28] and Sec. 3.2),
.
The binding energy is given by the seniority-model
expression (see Refs. [27,28] and Sec. 3.2),
![]() =0,
=0,![]() 1 selection rule for its matrix elements.
The expectation value of
1 selection rule for its matrix elements.
The expectation value of
![]() in the lowest
L=
in the lowest
L=
![]() state is:
state is:
![]() -1)/2 and L0=(2n+1-
-1)/2 and L0=(2n+1-![]() in Eq. (26). Assuming that the
odd particle occupies level n+1, this level is removed from the sum
of Eqs. (28) and (31),
i.e.,
one needs to consider the remaining
in Eq. (26). Assuming that the
odd particle occupies level n+1, this level is removed from the sum
of Eqs. (28) and (31),
i.e.,
one needs to consider the remaining ![]() levels only:
levels only:
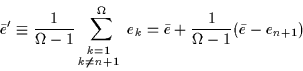
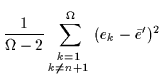
![$\displaystyle \sigma^2_e+\frac{1}{\Omega-2}\left[\sigma^2_e -\frac{\Omega}{\Omega-1}
(\bar{e}-e_{n+1})^2 \right].$](img96.gif)
![]() and
and
![]() in the strong pairing limit are given in
Sec. 3.2.
By adding the zero- and first-order contributions to
the binding energy, one obtains
the strong-pairing-limit expressions for
in the strong pairing limit are given in
Sec. 3.2.
By adding the zero- and first-order contributions to
the binding energy, one obtains
the strong-pairing-limit expressions for
![]() :
: