


Next: Results
Up: QUADRUPOLE INERTIA, ZERO-POINT CORRECTIONS,
Previous: The Model
In order to calculate the inertia tensor one usually applies the GOA
or uses the cranking model formalism. In both cases, the main task is
the calculation of mass tensors 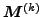 ,
,
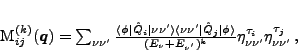 |
(7) |
where
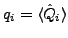 are the collective coordinates
(
are the collective coordinates
(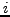 stands for
stands for 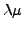 ),
),
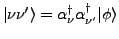 is a
two-quasiparticle state, and
is a
two-quasiparticle state, and 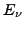 is the quasiparticle energy, and
is the quasiparticle energy, and
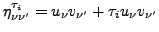 .
Factors
.
Factors 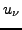 and
and 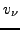 are the BCS amplitudes and the phase
are the BCS amplitudes and the phase
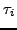 depends on the assumed definition of
depends on the assumed definition of 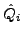 .
.
Both in the GOA and cranking, the inertia tensor
can be given by compact expressions[3,4]
![\begin{displaymath}
\bm B^{\rm GOA} = 2\bm\Sigma^{(2)}[\bm\Sigma^{(1)}]^{-1}\bm\Sigma^{(2)}\,,
\end{displaymath}](img48.png) |
(8) |
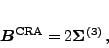 |
(9) |
where matrices
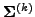 read
read
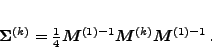 |
(10) |
In the nuclear case two kinds of fermions are present. The total
covariant inverse inertia for a composite system is given as a sum of
proton and neutron covariant inertia tensors [3]. This
leads to the final expression
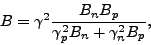 |
(11) |
where 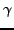 is the total metric tensor, which is a sum of proton
(
is the total metric tensor, which is a sum of proton
(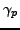 ) and neutron (
) and neutron (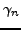 ) contributions.
) contributions.
We conclude this section by recalling that the zero-point energy in
the GOA can also be expressed through quantities
(10)[4], i.e.,
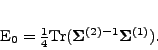 |
(12) |



Next: Results
Up: QUADRUPOLE INERTIA, ZERO-POINT CORRECTIONS,
Previous: The Model
Jacek Dobaczewski
2006-10-30
![]() ,
,