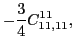 |
(34) | ||
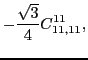 |
(35) |
In this Section, we assume the spherical, space-inversion, and time-reversal symmetries of the EDF, see Sec. IV of Ref. [2]. In this way we make our results applicable to the simplest case of spherical even-even nuclei. Below we fully show explicit results for the case of gauge symmetry conserved, whereas the full results pertaining to the case of Galilean symmetry are given in the supplemental material [24].
When the gauge symmetry is imposed on the EDF and the isospin degree of freedom is taken into account, we have 8 independent spherical EDF terms at second order, 6 at fourth order, and 6 at sixth order. The 8 corresponding second-order coupling constants can then be expressed by the 7 second-order pseudopotential parameters. Similarly, both at forth and sixth orders, 6 coupling constants can then be expressed by 6 pseudopotential parameters.
As is well known, at second order the isoscalar and isovector spin-orbit coupling
constants depend both on one spin-orbit pseudopotential parameter,
namely,
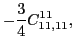 |
(34) | ||
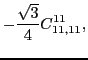 |
(35) |
|
|
0 | 5 | 0 | ||||
|
|
0 | 0 | |||||
|
|
3 | 0 | 5 | 0 | |||
|
|
0 | 0 | |||||
|
|
3 | ||||||
|
|
1 |
|
|
0 | 0 | |||||
|
|
15 | 0 | 0 | ||||
|
|
0 | 18 | 0 | ||||
|
|
0 | 18 | 0 | ||||
|
|
|||||||
|
|
|
|
|
0 | 0 | ||||
|
|
|
0 | 0 | ||||
|
|
|
0 | 0 | ||||
|
|
|
0 | 0 | ||||
|
|
|||||||
|
|
|
|
|
|
2 |
|
0 | 0 | |
|
|
|
|
2 | 0 | 0 | |
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
0 | 0 |
|
|
|
|
0 | 0 | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 | 0 | |
|
|
|
|
0 | 0 | ||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 | 0 |
|
|
|
|
|
2 | 0 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 | 0 | ||
|
|
|
|
0 | 0 | ||
|
|
|
|
|
|||
|
|
|
|
|
|
0 | 0 |
|
|
|
|
|
|
0 | 0 |
At second order, the gauge and Galilean symmetries are
equivalent to one another [2]. When at higher orders the Galilean invariance is imposed
on the spherical EDF, we have at fourth (sixth)
order 18 (32) independent terms, of which 4 (8) are of the spin-orbit
character. It turns out that, in the same way as for the second
order, the higher-order spin-orbit coupling constants are related
only to the spin-orbit pseudopotential parameters. Namely, at fourth
order we have
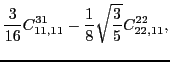 |
(37) | ||
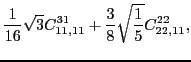 |
(38) | ||
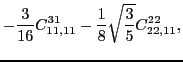 |
(39) | ||
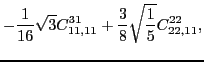 |
(40) |
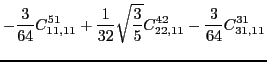 |
|||
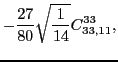 |
(43) | ||
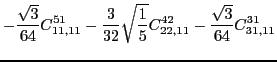 |
|||
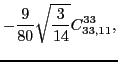 |
(44) | ||
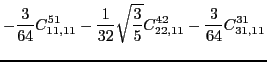 |
|||
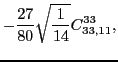 |
(45) | ||
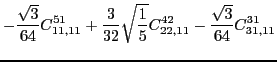 |
|||
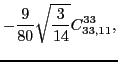 |
(46) | ||
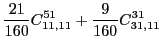 |
|||
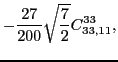 |
(47) | ||
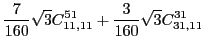 |
|||
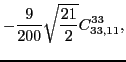 |
(48) | ||
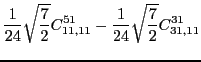 |
|||
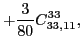 |
(49) | ||
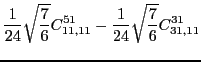 |
|||
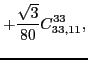 |
(50) |
If now we consider the Galilean-invariant and spherical EDF without
spin-orbit terms, we obtain at fourth (sixth) order 1 (2) possible
constraints among the remaining 14 (24) coupling constants related to
the remaining 13 (22) parameters of the pseudopotential. These
results are available in the supplemental material [24]. Of
course, such constraints can be imposed in very many different ways.
We have checked that, in fact, not any of the 1 (2) coupling
constants of the fourth (sixth) order spherical EDF can be considered
as being dependent on all the other coupling constants. In the
supplemental material we present one example of a possible choice,
whereby at fourth (sixth) order the coupling constants
![]() (
(
![]() and
and
![]() ) are selected to be dependent.
A comparison between the numbers of terms of the Galilean-invariant and gauge-invariant spherical
EDF with and without constraints coming from the reference to the pseudopotential is plotted in Fig. 2.
) are selected to be dependent.
A comparison between the numbers of terms of the Galilean-invariant and gauge-invariant spherical
EDF with and without constraints coming from the reference to the pseudopotential is plotted in Fig. 2.
![\includegraphics[width=7cm]{pseudo-fig2.eps}](img510.png) |