F. Raimondi, B.G. Carlsson, J. Dobaczewski
March 20, 2011
We derive a zero-range pseudopotential that includes all possible
terms up to sixth order in derivatives. Within the Hartree-Fock
approximation, it gives the average energy that corresponds to a
quasi-local nuclear Energy Density Functional (EDF) built of
derivatives of the one-body density matrix up to sixth order. The
direct reference of the EDF to the pseudopotential acts as a
constraint that divides the number of independent coupling
constants of the EDF by two. This allows, e.g., for expressing the isovector
part of the functional in terms of the isoscalar part, or vice
versa. We also derive the analogous set of constraints for the
coupling constants of the EDF that is restricted by spherical,
space-inversion, and time-reversal symmetries.
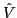order by order