


Next: Bibliography
Up: Effective pseudopotential for energy
Previous: Relations defining the gauge-invariant
Relations between the central-like and tensor-like pseudopotentials
In the following we present the recoupling formulae which connect the
two alternative forms of the pseudopotential of the Eqs. (1)
and (22). We have,
Analogously, the recoupling formula which allows to express the
tensor-like pseudopotential through the central-like one reads,
According to the recoupling of the Eq. (92), we give the list of the relations between the parameters of the two forms of the pseudopotential.
For the second order terms we have,
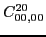 |
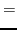 |
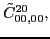 |
(94) |
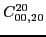 |
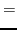 |
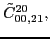 |
(95) |
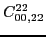 |
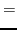 |
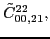 |
(96) |
 |
 |
 |
(97) |
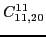 |
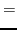 |
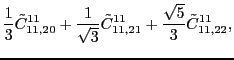 |
(98) |
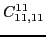 |
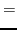 |
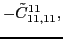 |
(99) |
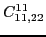 |
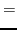 |
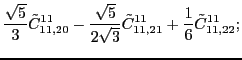 |
(100) |
at the fourth order,
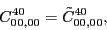 |
(101) |
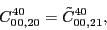 |
(102) |
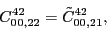 |
(103) |
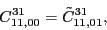 |
(104) |
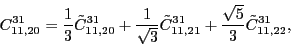 |
(105) |
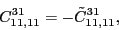 |
(106) |
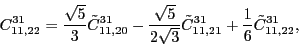 |
(107) |
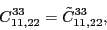 |
(108) |
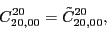 |
(109) |
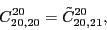 |
(110) |
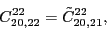 |
(111) |
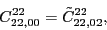 |
(112) |
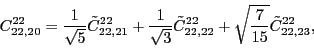 |
(113) |
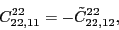 |
(114) |
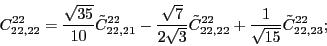 |
(115) |
at the sixth order,
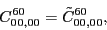 |
(116) |
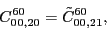 |
(117) |
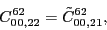 |
(118) |
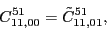 |
(119) |
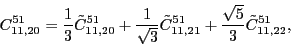 |
(120) |
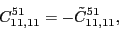 |
(121) |
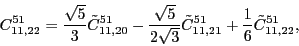 |
(122) |
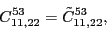 |
(123) |
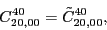 |
(124) |
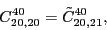 |
(125) |
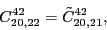 |
(126) |
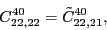 |
(127) |
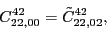 |
(128) |
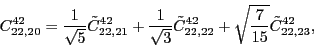 |
(129) |
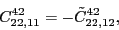 |
(130) |
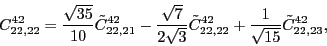 |
(131) |
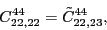 |
(132) |
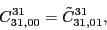 |
(133) |
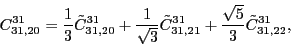 |
(134) |
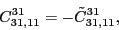 |
(135) |
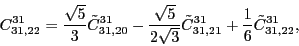 |
(136) |
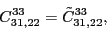 |
(137) |
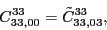 |
(138) |
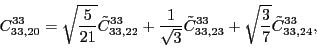 |
(139) |
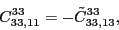 |
(140) |
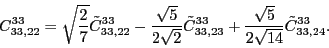 |
(141) |



Next: Bibliography
Up: Effective pseudopotential for energy
Previous: Relations defining the gauge-invariant
Jacek Dobaczewski
2011-03-20
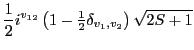
![$\displaystyle \left( \sum_{J=\vert\tilde{L}'-v_1\vert}^{\tilde{L}'+v_1} (-1)^{J...
... \left[K_{\tilde{n}\tilde{L}} \sigma^{(2)}_{v_2} \right]_{J}\right]_{0} \right.$](img601.png)
![$\displaystyle + \sum_{J=\vert\tilde{L}'-v_1\vert}^{\tilde{L}'+v_1} (-1)^{J+v_2+...
...ht]_{J}
\left[K_{\tilde{n}\tilde{L}} \sigma^{(1)}_{v_2} \right]_{J}\right]_{0}$](img602.png)
![$\displaystyle + \sum_{J=\vert\tilde{L}-v_1\vert}^{\tilde{L}+v_1}(-1)^{J+v_2+\ti...
...]_{J}
\left[K_{\tilde{n}'\tilde{L}'} \sigma^{(2)}_{v_2} \right]_{J}\right]_{0}$](img603.png)
![$\displaystyle + \left. \sum_{J=\vert\tilde{L}-v_1\vert}^{\tilde{L}+v_1}(-1)^{J+...
...left[K_{\tilde{n}'\tilde{L}'} \sigma^{(1)}_{v_2} \right]_{J}\right]_{0} \right)$](img604.png)