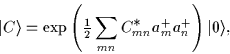Paper

The Bardeen-Cooper-Schrieffer (BCS) pairing theory [1], and its generalization by Bogolyubov [2], are based on fermion wave functions that have the form of fermion-pair condensates, i.e.,

$$\vert C\rangle = \exp\left({\textstyle{\frac{1}{2}}}\sum_{mn}C^{\displaystyle\ast}_{mn}a^+_m a^+_n\right)\vert\rangle,$$ (1)

where a⁺_m are the fermion creation operators, $\vert\rangle$ is the fermion vacuum, and C_mn is an antisymmetric complex matrix. Up to a unitary transformation of the single-particle basis,

$$\bar{a}^+_m = \sum_{m'}U^{\displaystyle\ast}_{mm'}a^+_{m'},$$ (2)

state (1) is equal to the so-called BCS state

$$\vert C\rangle = \prod_{m>0}\left(1+s_m c_m \bar{a}^+_{\tilde{m}}\bar{a}^+_m\right)\vert\rangle,$$ (3)

better known in its normalized form,

$$\frac{\vert C\rangle}{\langle{}C\vert C\rangle^{1/2}} = \pro... ...m+s_m v_m \bar{a}^+_{\tilde{m}}\bar{a}^+_m\right)\vert\rangle,$$ (4)

for

$$u_m = \frac{1}{\sqrt{1+c_m^2}}~~,~~v_m = \frac{c_m}{\sqrt{1+c_m^2}}~.$$ (5)

The Bloch-Messiah-Zumino theorem [3,4] provides the link between the two forms of state $\vert C\rangle$, Eqs. (1) and (3), by stating that every complex antisymmetric matrix can be brought by a unitary transformation into its canonical form, i.e.,

$$(U^TCU)_{mn} = s^{\displaystyle\ast}_nc_n\delta_{m\tilde{n}},$$ (6)

where index $\tilde{m}$ denotes the so-called canonical partner of the state m, the phase factors $s^{\displaystyle\ast}_n$=s^-1_n= $-s^{\displaystyle\ast}_{\tilde{n}}$have for the canonical partners opposite signs, and numbers c_n= $c_{\tilde{n}}$ are real and positive. Standard notation m>0, used in Eqs. (3) and (4), means that only one state is taken from each canonical pair. The proof of the theorem goes through a diagonalization of the hermitian matrix C⁺C, that yields the unitary transformation U and real, non-negative, pairwise degenerate eigenvalues c²_n.

When using states (1) in applications beyond the mean-field approximation, and in particular in the generator coordinate method (GCM) [5,6,7,8], the matrix elements and overlaps depend on the product matrix C⁺C'. For example, the overlap of two states (1) reads [9,6,8]

$$\langle{}C'\vert C\rangle = {\det}^{1/2}\left(1+C^+C'\right),$$ (7)

and the transition density matrix is given by [8]

$$\rho_{mn} = \frac{\langle{}C'\vert a^+_n a_m\vert C\rangle}{... ... C\rangle} = \left[\left(1+C^+C'\right)^{-1}C^+C'\right]_{mn}.$$ (8)

It has been realized long time ago [10] that the matrix C⁺C' is also pairwise degenerate, which facilitates calculation of the phase of the overlap, otherwise ambiguous because of the square root appearing in Eq. (7). Moreover, under certain conditions it has been proved in Ref. [11] that it is enough to give up the unitarity of matrix U to bring both matrices C and C' simultaneously into the canonical forms analogous to (6). The same fact has later been rediscovered in Ref. [12], although the necessary restrictions on matrices C and C' have not been recognized there.

In the present paper, I generalize results of Ref. [11] by deriving canonical forms of two arbitrary complex matrices C and C' in a common canonical basis. These results are not restricted by any conditions on matrices C and C'.

Let us begin by recalling the notion of the Jordan form (see e.g. [13]) of an arbitrary complex matrix. Focussing our attention on the matrix C⁺C', the vectors defining its Jordan basis can be arranged in columns of matrix W, and one has

$$\sum_{n}\left(C^+C'\right)_{mn}W_{ni}=\sum_j W_{mj}D_{ji},$$ (9)

where matrix D is block diagonal (composed of the Jordan blocks). One can attribute the number of the block I_i, the length of the block L_i, and the number within the block k_i, to every index i that numbers the Jordan basis vectors. In this notation, D has the form:

$$D_{ji}=\delta_{I_jI_i}D^{I_i}_{k_jk_i},$$ (10)

where in every block matrix D^I_kk' reads

$$D^{I}_{kk'}=D_I\delta_{kk'}+\delta_{kk'-1},$$ (11)

i.e., it has a common complex number D_I on the main diagonal and the ones just above the main diagonal.

Basis vectors belonging to a given block I form the so-called Jordan series of length L. The series starts with the basis vector called the series head, and ends with an eigenvector of C⁺C'. The whole series is uniquely determined by the series head, because the remaining basis vectors in the series can be obtained by a repeated action of C⁺C' on the series head. The basis vectors in a given series are not unique, because a linear combination of these vectors may give another valid series head, and leads to the same Jordan canonical form. Explicitly, this transformation reads

$$W'_{mk'}=\sum_{k=1}^L W_{mk}\alpha_{kk'}=\sum_{k=1}^{k'} W_{mk}\alpha_{L-k+1},$$ (12)

where the transformation matrix $\alpha_{kk'}$ depends on Larbitrary complex numbers $\alpha_k$ (only $\alpha_1$ must not vanish), and has the following explicit structure:

$$\alpha_{kk'} = \left(\begin{array}{lll@{~\ldots~}ll} \alp... ...lpha_2 \\ 0 & 0 & 0 & 0 & \alpha_1 \\ \end{array}\right).$$ (13)

It is easy to check that matrices having this structure form a group. It is also easy to check that vectors W'_mk form the Jordan series, similarly as vectors W_mk do, and that they can replace vectors W_mk in the Jordan basis, giving the same matrix D in Eq. (9).

According to the Jordan construction, the whole space in which acts matrix C⁺C' splits into subspaces spanned by the Jordan series. The number of eigenvectors of C⁺C' equals to the number of different series, or to the number of Jordan blocks, and is in general smaller than the dimension of the matrix C⁺C'. Some matrices (hermitian or not) can be fully diagonalized, i.e., they have numbers of eigenvectors equal to their dimensions. This corresponds to the case when all the Jordan series have the length equal 1.

One calls two blocks degenerate, or two series degenerate, if they have the same diagonal number D_I, and they have the same length L. The latter condition is very important, because only degenerate series defined in such a way can be mixed; this is an analogue of the possibility to mix degenerate eigenvectors of a matrix which can be fully diagonalized. If two series have different lengths then vectors of a longer series cannot be admixed to those of the shorter series, even if the series have the same diagonal number D_I. If the matrix can be fully diagonalized, then all the series have length 1, the number of eigenvectors equals to the dimension of C⁺C', and transformation (12) reduces to the possibility of arbitrarily normalizing every eigenvector.

After these necessary preliminaries, let us proceed with presenting the main results of the present paper. Multiplying from the left-hand and right-hand sides the eigen-equation (9) by W^-1, and then transposing, we obtain that

$$C'\left(C^+{W^{-1}}^T\right)={W^{-1}}^T D^T\;,$$ (14)

which multiplied by C⁺ from the left-hand side gives

$$\left(C^+C'\right)\left(C^+{W^{-1}}^T\right) =\left(C^+{W^{-1}}^T\right)D^T\;.$$ (15)

One can see now that matrix C⁺C' has another equivalent set of Jordan series, i.e.,

$$\sum_{n}\left(C^+C'\right)_{mn}V_{ni}=\sum_j V_{mj}D_{ji},$$ (16)

where the new matrix of basis vectors V is given by

 

V=C⁺W^-1T J. (17)

In every Jordan block, matrix J has the ones on the skew diagonal and zeros otherwise, i.e., J_kk'= $\delta_{k,L-k'+1}$. Hence, when an arbitrary matrix is multiplied by J from the right-hand (left-hand) side, the order of its columns (rows) is flipped. In particular, one obtains that D^T=JDJ.

We can now analyze cases of different degeneracies of the Jordan blocks. The arguments given below closely follow proofs presented in Ref. [11], only with the degeneracies of eigenvalues replaced by the degeneracies of the Jordan blocks.

Let us first suppose that C⁺C' has a non-degenerate Jordan block. Then, in this block the basis vectors V must be connected with the basis vectors W by transformation (12), i.e.,

$$\left(C^+{W^{-1}}^T J\right)_{mk'} = \sum_{k=1}^L W_{mk}\alpha_{kk'}.$$ (18)

Multiplying Eq. (18) by W^-1 from the left-hand side, and by J from the right-hand side, one obtains

$$\left(W^{-1}C^+{W^{-1}}^T\right)_{kk'} = \left(\alpha J\right)_{kk'}.$$ (19)

However, the matrix on the left-hand side of this equation is antisymmetric, while that on the right-hand side is symmetric; therefore, matrix $\alpha_{kk'}$ must vanish. This requires that, in a non-degenerate Jordan block, all vectors Vvanish, which contradicts Eq. (14), unless the block has length L=1 and D_I=0. Therefore, matrix C⁺C' cannot have non-degenerate Jordan blocks apart from the subspace of L=1 eigenvectors with all eigenvalues equal zero.

One can set this subspace aside, and assume from now on that C⁺C'is non-singular and has an even dimension. In this case, matrix C⁺C' cannot have any non-degenerate Jordan block, and hence Jordan blocks must appear in degenerate pairs. (In odd dimensions, C⁺C'must have at least one null eigenvalue, which can be separated, and the remaining matrix can be treated in the even dimension).

In the present considerations, it is enough to consider only pairs of degenerate blocks; had the higher degeneracies of the Jordan blocks occurred, one could have considered one pair after another, and at each step one could reduce the dimension of the problem. This is possible here, and has not been possible when considering degenerate eigenvalues in Ref. [11], because the whole space can be separated into the subspaces corresponding to the Jordan blocks, while it cannot be separated into subpaces corresponding to the eigenvalues.

Let us now consider a pair of degenerate Jordan blocks, each block having length L and the common diagonal element D_I= $D_{\tilde{I}}$. One can adopt here the standard notation that originally pertains to the canonical pairs, namely, we denote the indices of the two degenerate blocks by I and $\tilde{I}$. Similarly, indices inside these two blocks are denoted by k=1, 2,...,L and $\tilde{k}$=1, 2,...,L, respectively. Note that vectors in these two blocks form series, i.e., they are arranged in a specific order; therefore a vector at a given position must be associated with the vector at the same position in the second block.

Since for matrix C⁺C' two equivalent Jordan bases exist, W and V, vectors in series V must be linear combinations of those in series W. In the pair of degenerate Jordan blocks, this leads to the following relations between the two series:

  

$$\left(C^+{W^{-1}}^T J\right)_{mk'} \!\sum_{k =1}^L W_{mk }\alpha_{kk'} + \sum_{\tilde{k}=1}^L W_{m\tilde{k}} \beta_{kk'},$$ = (20)

$$\left(C^+{W^{-1}}^T J\right)_{m\tilde{k}'} \!\sum_{k =1}^L W_{mk }\gamma_{kk'} + \sum_{\tilde{k}=1}^L W_{m\tilde{k}}\epsilon_{kk'},$$ = (21)

All the four matrices $\alpha$, $\beta$, $\gamma$, and $\epsilon$have the same structure (13). One may now proceed with multiplying Eqs. (20) and (21) from the left-hand side either by W^-1_km or by $W^{-1}_{\tilde{k}m}$, and from the right-hand side by J. Since all matrices $\alpha{J}$, $\beta{J}$, $\gamma{J}$, and $\epsilon{J}$ are symmetric, one then obtains that $\alpha$=$\epsilon$=0 and $\gamma$=$-\beta$.

Therefore, the canonical form of the C⁺ matrix reads

$$\left({W^{-1}} C^+ {W^{-1}}^T\right)_{ji} =s_{I_j}C^{I_j\,+}_{k_jk_i} \delta_{I_j\tilde{I}_i},$$ (22)

where the symmetric matrix C^I= $C^{\tilde{I}}$ occupies the off-diagonal part in every pair of the degenerate Jordan blocks, and

$$C^{I} = s_I\beta^{\displaystyle\ast} J ,$$ (23)

for $\beta$ having form (13). Following the standard notation, we have defined the phase factors s_I= $-s_{\tilde{I}}$in such a way that the skew-diagonal matrix elements of C^I (that are all equal one to another) are real and positive, i.e., C^I_k,L-k+1>0.

Since the canonical basis of C⁺ is the same as the Jordan basis of C⁺C', matrix C' must in the very same basis assume an analogous canonical form:

$$\left(W^T C' W\right)_{ji} = s_{I_i}^{\displaystyle\ast} C'^{I_i}_{k_jk_i} \delta_{I_j\tilde{I}_i},$$ (24)

where the symmetric matrix C'^I= $C'^{\tilde{I}}$ reads

$$C'^{I} = s_I^{\displaystyle\ast}J \beta'^{\displaystyle\ast}$$ (25)

and $\beta'$ has also form (13). Finally, in order to satisfy Eq. (9) matrices $\beta$ and $\beta'$ must obey the following condition:

$$\beta \beta'^{\displaystyle\ast} = D .$$ (26)

This leaves us still some freedom in the choice of the canonical basis, because any solution of Eq. (26) gives one valid canonical form. Two obvious choices are, for example, $\beta$=D and $\beta'^{\displaystyle\ast}$=Ior $\beta$=$\sqrt{D}$ and $\beta'^{\displaystyle\ast}$=$\sqrt{D}$, where any one of the possible branches of the matrix square root can be taken.

Equations (22) and (24) complete the proof of the canonical forms of two arbitrary complex antisymmetric matrices C and C'. Both these matrices can be simultaneously transformed by matrix W (in general non-unitary) into the block-diagonal forms with non-zero elements only between pairs of degenerate Jordan blocks.

Needless to say, whenever matrix C⁺C' can be fully diagonalized, which was the case in Ref. [11], both matrices C and C'acquire in the canonical basis the standard canonical forms analogous to Eq. (6), i.e.,

$$\left({W^{-1}} C^+ {W^{-1}}^T\right)_{ji} =s_j c_{j}^{\displaystyle\ast}\delta_{j\tilde\imath}\;,$$ (27)

and

$$\left(W^T C' W\right)_{ji} =s_i^{\displaystyle\ast} c'_{i}\delta_{j\tilde\imath}\;,$$ (28)

where $c_{i}^{\displaystyle\ast}c'_{i}$=D_i.

In Ref. [14] it was noticed that an incorrect conjecture was formulated in Ref. [11], namely, the conjecture that the simple forms of Eqs. (27) and (28) can always be achieved. In the present study we have seen that these simple forms occur only when matrix C⁺C' can be fully diagonalized. In fact, this is the case which occurs most often in applications. Therefore, let us now discuss conditions for the full diagonalization of C⁺C'.

In the applications given in Ref. [11], the full diagonalization of matrix C⁺C' was secured by using a model in which matrices C were time-even,

 

C⁺=U_TC^TU_T^T, (29)

and the Hermitian and time-even matrices $\tilde{C}$ defined by

$$\tilde{C}= -U_TC$$ (30)

were positive definite. In these equations, U_T is a unitary and antisymmetric matrix, U_T⁺=U_T^-1= $-U_T^{\displaystyle\ast}$. The positive definiteness of matrices $\tilde{C}$ was in [11] guaranteed by a special form of matrices C. In that study, the GCM states were constructed within the SCEM model [15,16], and therefore matrices C had the form shown in Eq. (2.13) of [11]. Therefore, the corresponding $\tilde{C}$ matrices were all equal to exponents of hermitian matrices, and hence trivially positive definite.

In the general presentation of the present paper, conditions (29) and (30) can be formulated as follows: If there exist a unitary antisymmetric matrix U_T such that Eq. (29) holds for C and C', and at the same time at least $\tilde{C}$ or $\tilde{C'}$ is positive-definite, then matrix C⁺C' can be fully diagonalized, and the simple canonical forms (27) and (28) exist. The proof of this statement has been given in Ref. [11] (Appendix C), and will not be repeated here.

The positive definiteness of $\tilde{C}$ is a required condition, because the hermitian square-root of $\tilde{C}$ must exist. Unfortunately, this condition cannot be released, i.e., if both $\tilde{C}$ and $\tilde{C'}$ are not positive definite, it may happen that matrix C⁺C' cannot be fully diagonalized. An example of such a situation is provided by the following two 4$\times$4 matrices:

$$C = \left(\begin{array}{cc} 0 & A \\ -A^T & 0 \end{array}... ...t(\begin{array}{cc} 0 & A'\\ -A'^T & 0 \end{array}\right) ,$$ (31)

where the two-dimensional matrices A and A' read

$$A = \left(\begin{array}{cc} 1 & a \\ a^{\displaystyle\ast... ...\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) .$$ (32)

For the standard time-reversal matrix U_T given by

$$U_T = \left(\begin{array}{cc} 0 & I \\ -I & 0 \end{array}... ...eft(\begin{array}{cc} A^T & 0 \\ 0 & A \end{array}\right) ,$$ (33)

and $\tilde{C'}$ has the same form. Neither $\tilde{C}$(for a$\neq$0) nor $\tilde{C'}$ is positive definite, and the C⁺C'= $\tilde{C}\tilde{C}'$ matrix,

$$C^+C' = \left(\begin{array}{cc} (AA')^{\displaystyle\ast} ... ...cc} a & 1 \\ 0 & a^{\displaystyle\ast} \end{array}\right) ,$$ (34)

cannot be fully diagonalized, unless a$\neq$ $a^{\displaystyle\ast}$.

However, for any small but non-zero imaginary part of a, matrix C⁺C' can be fully diagonalized. Therefore, this example also shows that the positive definiteness of (time-even) matrices $\tilde{C}$ or $\tilde{C'}$ is only a sufficient condition for the full diagonalization of C⁺C'= $\tilde{C}\tilde{C}'$, but it is not necessary. Moreover, it is clear that matrix C⁺C' cannot be diagonalized for a= $a^{\displaystyle\ast}$, because in the limit of $\Im{a}$ $\longrightarrow$0 two eigenvectors of C⁺C' become parallel. This illustrates the difficulty of diagonalizing C⁺C'numerically for small values of $\Im{a}$; the task is then bound to become ill-conditioned.

In the GCM, matrices C are most often obtained from solutions of the Hartree-Fock-Bogoliubov (HFB) or Hartree-Fock+BCS [8] equations for time-even states. In these cases, matrices $\tilde{C}$ are diagonal in the HFB or BCS canonical bases [8] (composed of pairs of time-reversed states), and their eigenvalues are equal to v_m/u_m=c_m, where v_m and u_m are the standard quasiparticle amplitudes of Eq. (5). Here, the canonical pairs are defined by the time reversal, and therefore the eigenvalues c_m, can have, in principle, arbitrary signs.

However, in the BCS method (with a constant gap parameter $\Delta$) all these quasiparticle amplitudes are positive, and hence all the resulting $\tilde{C}$ matrices are positive definite, thus fulfilling the sufficient condition for the full diagonalization of C⁺C'= $\tilde{C}\tilde{C}'$. In fact, quasiparticle amplitudes of different signs rarely occur in nuclear physics applications, cf. Ref. [17]. This is so, because typical pairing forces couple the time-reversed states, and, in general, are always attractive. This shows that the Jordan structures discussed here cannot be expected to be frequently encountered, and most often one will deal with the standard canonical forms of Eqs. (27) and (28), in which the only non-zero matrix elements are adjacent to the main diagonal.

In summary, I have shown how to extend the results of Ref. [11] in order to construct canonical basis in which two arbitrary complex antisymmetric matrices C and C' acquire simultaneously canonical forms. This construction completes the generalization of the classic Bloch-Messiah-Zumino theorem to the case of non-diagonal matrix elements calculated between fermion-pair condensates.

The critical reading of the manuscript by S.G. Rohozinski is gratefully appreciated. This research was supported by the Polish Committee for Scientific Research, Contract No. 2 P03B 040 14.