

Next: About this document ...
Up: Superdeformed bands in S
Previous: Bibliography
Figure 1:
Neutron single-particle routhians in the magic SD
configuration of 32S calculated within the HF theory
for the Skyrme SLy4
interaction. Lines denoting the four (parity,
signature) combinations are: solid (+,+i), dot-dashed
(+,-i), dotted (-,+i), and dashed (-,-i).
Standard Nilsson labels are determined by finding the
dominating HO components of the HF wave-functions at
low (left set) and high (right set) rotational frequencies.
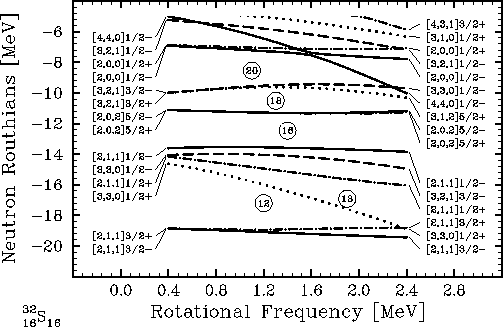 |
Figure 2:
Same as Fig. 1, but for the proton
single-particle routhians.
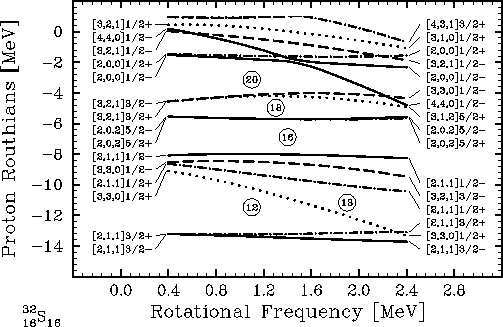 |
Figure:
Schematic diagram illustrating the single-particle
neutron or proton orbitals (top), and the corresponding
many-particle configurations (bottom), relevant for the
description of SD bands in 32S. The top part gives the
Nilsson labels and signatures (r=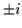 ), inside the
circles, of orbitals on both sides of the N=16 or
Z=16 Fermi level. Four labels on the left-hand side
represent the N0=3 intruder states (negative parity), and four on
the right-hand side represent positive-parity states. In the
bottom part, the full circles stand for occupied, the
open circles for empty states. Symbols 3n/p give
numbers n or p of (neutron or proton) occupied
intruder states. Subscripts
), inside the
circles, of orbitals on both sides of the N=16 or
Z=16 Fermi level. Four labels on the left-hand side
represent the N0=3 intruder states (negative parity), and four on
the right-hand side represent positive-parity states. In the
bottom part, the full circles stand for occupied, the
open circles for empty states. Symbols 3n/p give
numbers n or p of (neutron or proton) occupied
intruder states. Subscripts 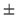 indicate whether the
number of particles in the positive-parity r=+iorbitals is larger than that in r=-i orbitals, or
vice versa.
indicate whether the
number of particles in the positive-parity r=+iorbitals is larger than that in r=-i orbitals, or
vice versa.
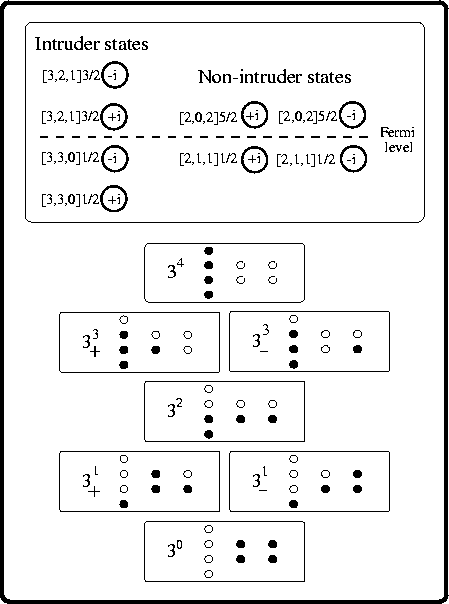 |
Figure 4:
Same as Fig. 1, but for the HF solution with the
31-31- configuration.
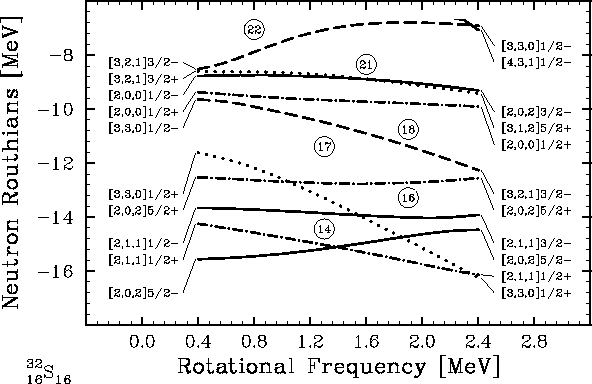 |
Figure 5:
Same as Fig. 1, but for the HF solution with the
31+31+ configuration.
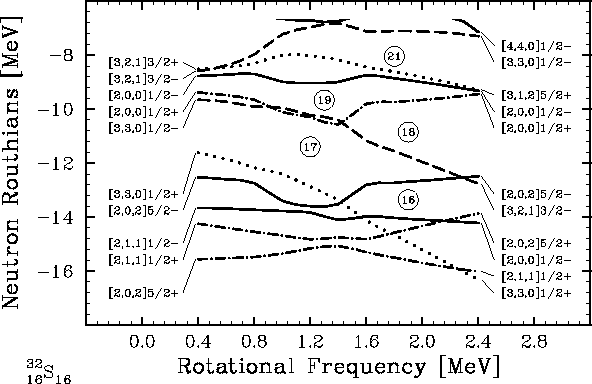 |
Figure:
Energies of the HF bands in 32S as functions of the angular momentum.
A rigid-rotor reference energy of 0.05I(I+1)MeV has
been subtracted to increase clarity of the plot. Full
and open symbols represent the positive- (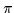 =+1) and
negative-parity (
=+1) and
negative-parity (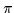 =-1) bands. Long-short-dashed,
solid, dotted, and dashed lines correspond to neutron
(rn) and proton (rp) signatures being equal to,
respectively, (rn,rp)=(+,+), (+,-), (-,+),
and (-,-). Note that for even numbers of protons and
neutrons the possible total signatures are
=-1) bands. Long-short-dashed,
solid, dotted, and dashed lines correspond to neutron
(rn) and proton (rp) signatures being equal to,
respectively, (rn,rp)=(+,+), (+,-), (-,+),
and (-,-). Note that for even numbers of protons and
neutrons the possible total signatures are 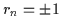 and
and
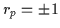 ;
the latter should not be confused with the
single-nucleon signatures taking the possible values of
;
the latter should not be confused with the
single-nucleon signatures taking the possible values of 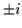 .
.
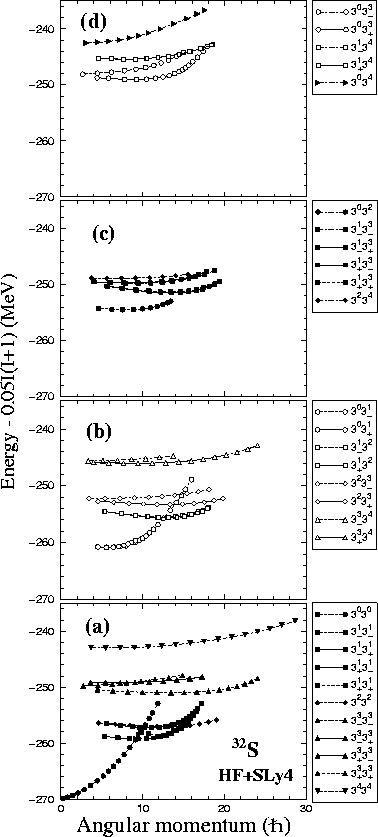 |
Figure 7:
Same as in Fig. 6, but for the yrast region
of energies.
 |
Figure:
Proton quadrupole moments of the HF bands in 32S,
shown in the form of points on the Q20-Q22 plane.
Since the variation of the multipole moments in function of
the rotational frequency turns out to be regular the corresponding points
form trajectories.
Arrows indicate directions of increasing
 .
Note a large difference in scale between the Q20 and Q22axes. The scales were adapted to the large differences between
|Q20| and |Q22|.
The straight lines corresponding to
.
Note a large difference in scale between the Q20 and Q22axes. The scales were adapted to the large differences between
|Q20| and |Q22|.
The straight lines corresponding to 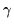 =
=
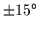 and to
and to
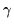 =
=
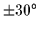 have been drawn to facilitate reading the degree
of non-axiality of the corresponding solutions.
have been drawn to facilitate reading the degree
of non-axiality of the corresponding solutions.
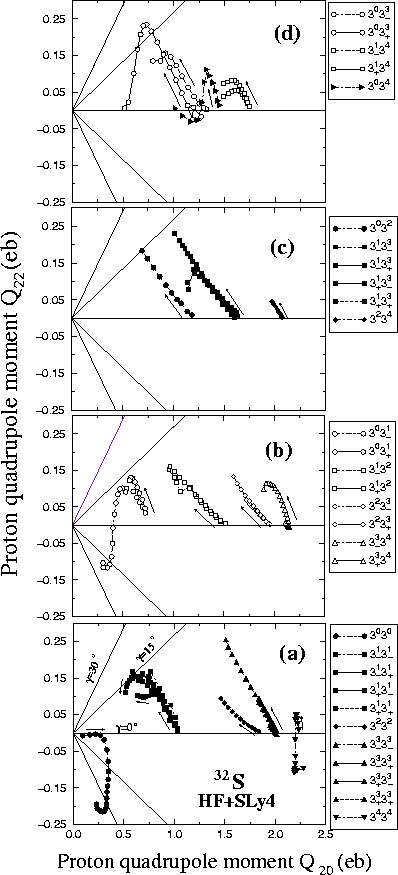 |
Figure:
Dynamical moments
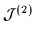 of the HF bands in 32S
as functions of the
rotational frequency. The figure shows results for near-yrast
bands selected in Fig. 7.
of the HF bands in 32S
as functions of the
rotational frequency. The figure shows results for near-yrast
bands selected in Fig. 7.
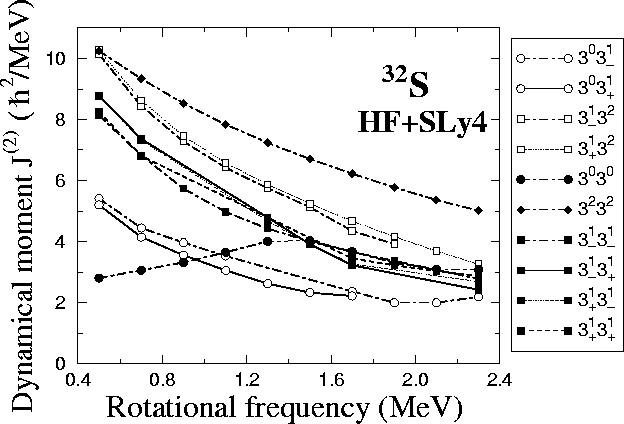 |
Figure:
Relative alignments 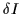 of the HF bands in 32S
as functions of the
rotational frequency, calculated with respect to the SD magic
band in 32S.
The figure shows results for near-yrast
bands selected in Fig. 7.
of the HF bands in 32S
as functions of the
rotational frequency, calculated with respect to the SD magic
band in 32S.
The figure shows results for near-yrast
bands selected in Fig. 7.
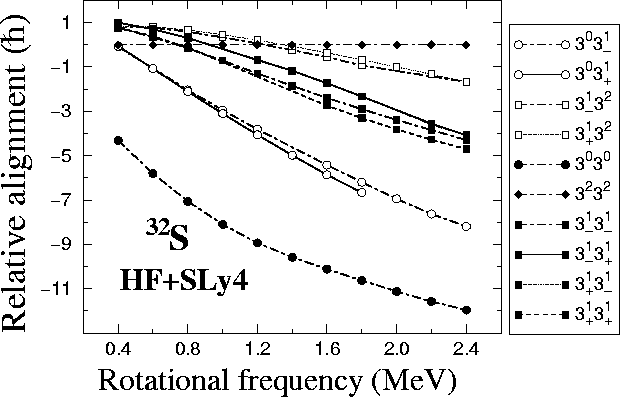 |
Figure:
Energies of the HF bands in 33S and 31S as functions of the
angular momentum.
A rigid-rotor reference energy of 0.05I(I+1)MeV has
been subtracted to increase clarity of the plot. Full
and open symbols represent the positive- (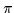 =+1) and
negative-parity (
=+1) and
negative-parity (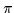 =-1) bands. Long-short-dashed and
solid lines denote signatures r=+i and r=-i,
respectively. Configurations 31* and 33* correspond to
the highest negative-parity particles promoted to the next-to-lowest available
intruder states. For 31*, the first point corresponds to
=-1) bands. Long-short-dashed and
solid lines denote signatures r=+i and r=-i,
respectively. Configurations 31* and 33* correspond to
the highest negative-parity particles promoted to the next-to-lowest available
intruder states. For 31*, the first point corresponds to
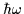 =0.6MeV.
=0.6MeV.
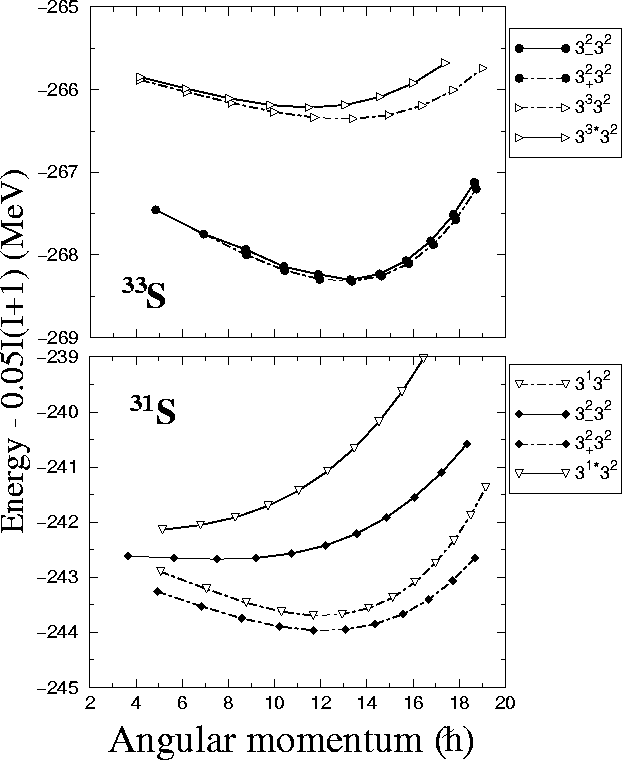 |
Figure 12:
Same as in Fig. 11, but for the 33Cl and 31P
nuclei.
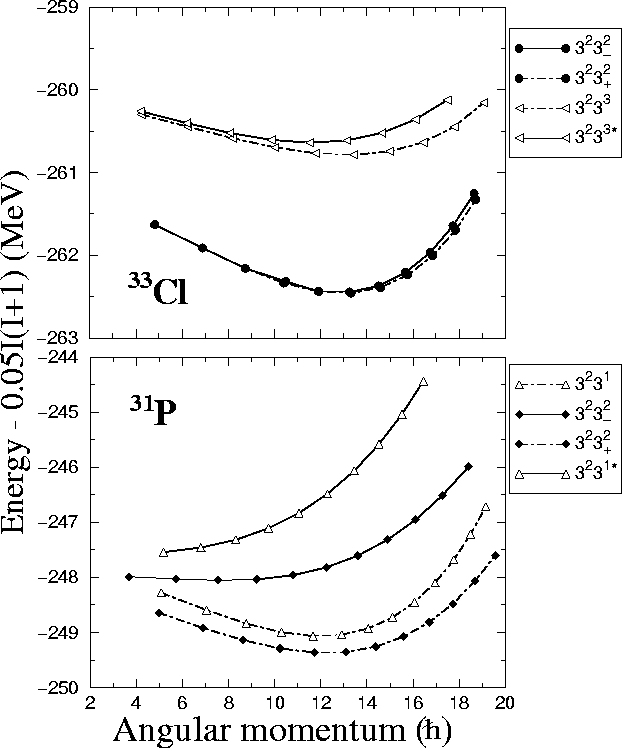 |
Figure:
Same as in Fig. 11, but for the dynamical moments
 .
.
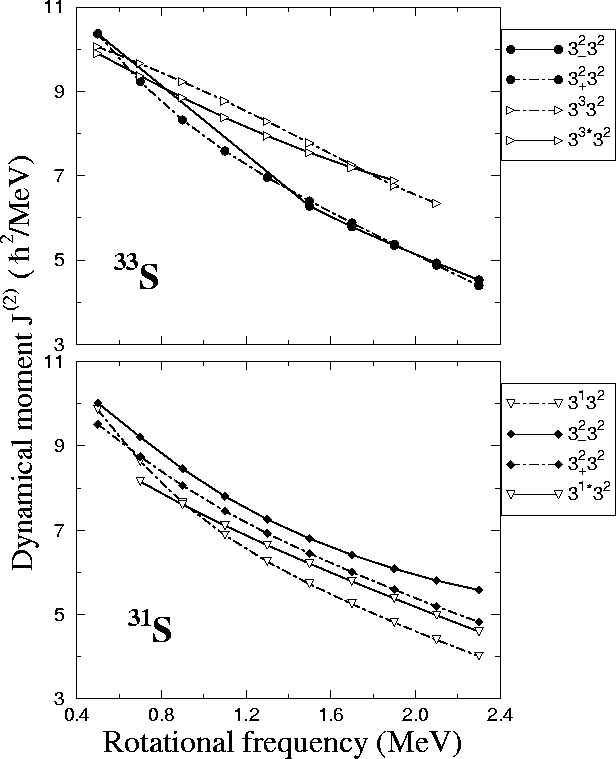 |
Figure 14:
Same as in Fig. 13, but for the 33Cl and 31P
nuclei.
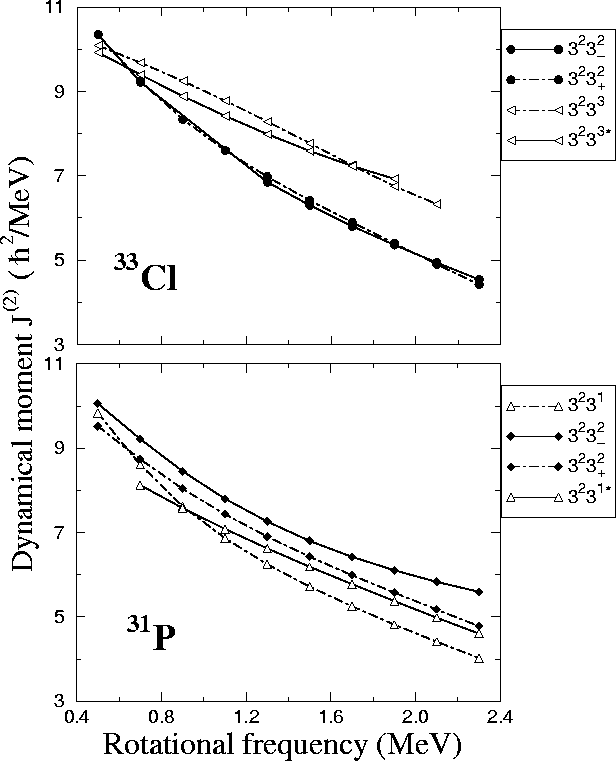 |
Figure:
Relative alignments  of the HF bands in 33S, 31S, 33Cl, and 31P
as functions of the
rotational frequency, calculated with respect to the SD magic
band in 32S (see Fig. 11 for conventions used for
symbols and lines).
The Nilsson labels of particle (p) or hole (h) orbitals,
which make the difference between the given band and the magic band
in 32S, are indicated on the right-hand side.
of the HF bands in 33S, 31S, 33Cl, and 31P
as functions of the
rotational frequency, calculated with respect to the SD magic
band in 32S (see Fig. 11 for conventions used for
symbols and lines).
The Nilsson labels of particle (p) or hole (h) orbitals,
which make the difference between the given band and the magic band
in 32S, are indicated on the right-hand side.
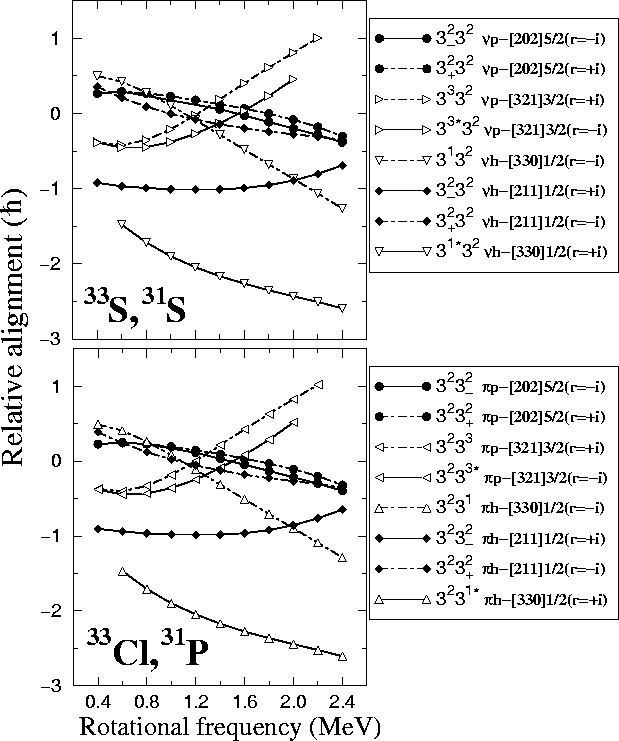 |
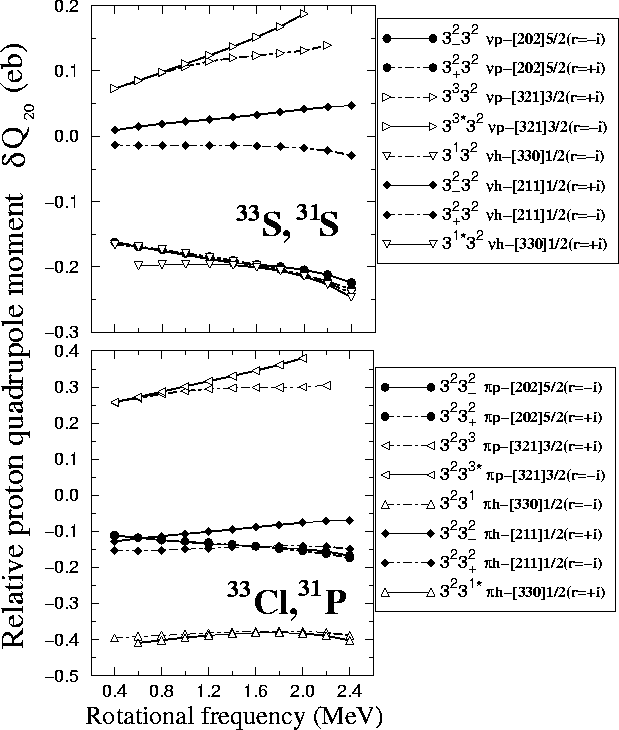
Figure:
Same as in Fig. 15,
but for the relative proton quadrupole moments
 .
.
 |


Next: About this document ...
Up: Superdeformed bands in S
Previous: Bibliography
Jacek Dobaczewski
1999-07-27








