

Next: Single group D for
Up: Symmetry operators
Previous: Symmetry operators
Fock-space representations
It will be convenient to use the Cartesian representation of the
symmetry operators. Let 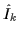 for k=x,y,z denote the
Cartesian components of the total angular momentum operator
(generators of the group of rotations).
In the coordinate-space representation these operators read (
for k=x,y,z denote the
Cartesian components of the total angular momentum operator
(generators of the group of rotations).
In the coordinate-space representation these operators read (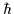 =1)
=1)
 |
(1) |
where
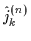 ,
,
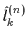 ,
and
,
and
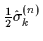 are operators of the total, orbital, and
intrinsic angular momenta, respectively, of particle number n. By
definition, operators (1) act in the Hilbert space
are operators of the total, orbital, and
intrinsic angular momenta, respectively, of particle number n. By
definition, operators (1) act in the Hilbert space
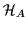 of A-particle states, and the number of particles
A appears explicitly in their definitions.
of A-particle states, and the number of particles
A appears explicitly in their definitions.
One can use another representations of 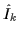 ,
the so-called second-quantized, or Fock-space form,
,
the so-called second-quantized, or Fock-space form,
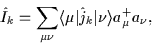 |
(2) |
where
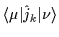 are the matrix elements of the angular-momentum
operators in the single-particle basis defined by the fermion
creation and annihilation operators
are the matrix elements of the angular-momentum
operators in the single-particle basis defined by the fermion
creation and annihilation operators 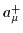 and
and 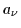 .
Operators
.
Operators
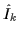 in the form of Eq. (2) do not explicitly depend on
A, and act simultaneously in all the A-particle spaces, i.e., they
act in the Fock space
in the form of Eq. (2) do not explicitly depend on
A, and act simultaneously in all the A-particle spaces, i.e., they
act in the Fock space 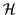 ,
,
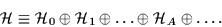 |
(3) |
In each subspace
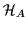 ,
operators (2) are equal
to (1). Since both act in different domains, one should, in
principle, denote them with different symbols. However, one usually
understands definition (1) as a prescription to construct
,
operators (2) are equal
to (1). Since both act in different domains, one should, in
principle, denote them with different symbols. However, one usually
understands definition (1) as a prescription to construct
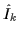 for all values of A simultaneously (adjoined by
for all values of A simultaneously (adjoined by
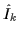
 0 for A=0). With this extension, operators
(1) and (2) are equal. In this section we understand
that all operators act in the Fock space (3), while the
corresponding definitions are given in the coordinate-space
representation.
0 for A=0). With this extension, operators
(1) and (2) are equal. In this section we understand
that all operators act in the Fock space (3), while the
corresponding definitions are given in the coordinate-space
representation.
We introduce three standard
transformations
of rotation around three mutually perpendicular axes,
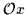 ,
,
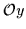 and
and
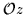 ,
through the angles of
,
through the angles of 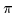 as
as
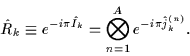 |
(4) |
Similarly, we introduce three operators of reflection
in planes yz, zx, and xy, for k=x,y,z,
respectively, which can be written as
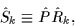 |
(5) |
where the inversion operator is denoted by 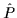 .
The order of operators in Eq. (5) is unimportant because
.
The order of operators in Eq. (5) is unimportant because
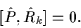 |
(6) |
Finally, the (antilinear) time-reversal operator in the
coordinate-space representation is defined as [15]:
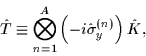 |
(7) |
where 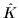 is the complex conjugation operator associated with the
coordinate representation.
is the complex conjugation operator associated with the
coordinate representation.
In what follows it will be convenient to denote with separate
symbols the products of 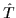 with
with 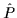 ,
,
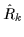 ,
and
,
and
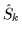 [16], i.e., the seven additional
(apart from
[16], i.e., the seven additional
(apart from 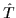 itself) antilinear
operators read
itself) antilinear
operators read
The order of multiplications in the
above definitions is irrelevant since
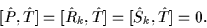 |
(11) |
In nuclear physics applications the linear operators 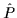 ,
,
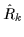 ,
and
,
and
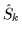 are usually referred to as inversion,
signature, and simplex. The antilinear operators
are usually referred to as inversion,
signature, and simplex. The antilinear operators 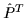 ,
,
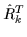 ,
and
,
and
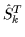 will be called T-inversion,
T-signature, and T-simplex, respectively.
will be called T-inversion,
T-signature, and T-simplex, respectively.
For completeness, yet two another operators must be added to the
above symmetry operators. One of them is, of course, the identity
operator, 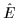 ,
which can be treated as the rotation through angle
equal to 0 or
,
which can be treated as the rotation through angle
equal to 0 or 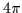 about an arbitrary axis. The second one is the
rotation through angle
about an arbitrary axis. The second one is the
rotation through angle 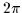 about an arbitrary axis, i.e.,
about an arbitrary axis, i.e.,
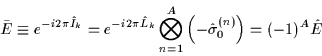 |
(12) |
where
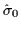 is the unity
is the unity 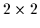 matrix. We see that
only for even systems
matrix. We see that
only for even systems 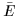 is equal to identity, while for odd
systems it is equal to the minus identity. We should keep in mind, that in
the group theory there is no such a notion as a change of sign.
Operators like (-1)A may appear in representations, like here they
do appear in the Fock-space representation, however, one cannot use
them when defining the group structures in Secs. 2.2 and
2.3 below.
is equal to identity, while for odd
systems it is equal to the minus identity. We should keep in mind, that in
the group theory there is no such a notion as a change of sign.
Operators like (-1)A may appear in representations, like here they
do appear in the Fock-space representation, however, one cannot use
them when defining the group structures in Secs. 2.2 and
2.3 below.
To investigate multiplication rules of the symmetry operators
introduced above one explicitly calculates products of them. For
example, the products of two signatures are
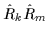 |
= |
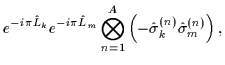 |
(13) |
and the square of the time reversal reads
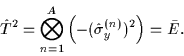 |
(14) |
It is obvious that these results depend on whether A is even or odd.
Therefore, in what follows we introduce notation which explicates
whether the operators act in even or odd fermion spaces,
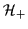 or
or
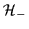 ,
,
Any Fock-space operator
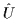 :
: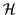
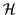 ,
which conserves the particle number, is split into two parts
with different domains, i.e.,
,
which conserves the particle number, is split into two parts
with different domains, i.e.,
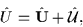 |
(17) |
where the bold symbols denote operators which act in the even-A spaces,
while the script symbols denote those acting in the odd-A spaces, i.e.,
With these definitions we are now in a position to investigate the
group structures appearing for the introduced operators.


Next: Single group D for
Up: Symmetry operators
Previous: Symmetry operators
Jacek Dobaczewski
2000-02-05
![]() for k=x,y,z denote the
Cartesian components of the total angular momentum operator
(generators of the group of rotations).
In the coordinate-space representation these operators read (
for k=x,y,z denote the
Cartesian components of the total angular momentum operator
(generators of the group of rotations).
In the coordinate-space representation these operators read (![]() =1)
=1)
![]() ,
the so-called second-quantized, or Fock-space form,
,
the so-called second-quantized, or Fock-space form,
![]() ,
,
![]() and
and
![]() ,
through the angles of
,
through the angles of ![]() as
as
![]() with
with ![]() ,
,
![]() ,
and
,
and
![]() [16], i.e., the seven additional
(apart from
[16], i.e., the seven additional
(apart from ![]() itself) antilinear
operators read
itself) antilinear
operators read
![]() ,
,
![]() ,
and
,
and
![]() are usually referred to as inversion,
signature, and simplex. The antilinear operators
are usually referred to as inversion,
signature, and simplex. The antilinear operators ![]() ,
,
![]() ,
and
,
and
![]() will be called T-inversion,
T-signature, and T-simplex, respectively.
will be called T-inversion,
T-signature, and T-simplex, respectively.
![]() ,
which can be treated as the rotation through angle
equal to 0 or
,
which can be treated as the rotation through angle
equal to 0 or ![]() about an arbitrary axis. The second one is the
rotation through angle
about an arbitrary axis. The second one is the
rotation through angle ![]() about an arbitrary axis, i.e.,
about an arbitrary axis, i.e.,
![]() or
or
![]() ,
,