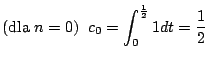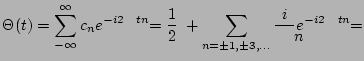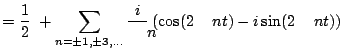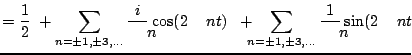Przykład 2.1
Policzmy postać współczynników Fouriera dla funkcji  (rys. 2.1),
określonej na przedziale
(rys. 2.1),
określonej na przedziale ![$ [0,1]$](img159.png) w następujący sposób:
w następujący sposób:
![$\displaystyle \Theta(t) = \left\{ \begin{array}{rcl} 1 &, & t \in [0, \frac{1}{2})\\ 0 &, & t \in [ \frac{1}{2}, 1] \end{array} \right.$](img160.png) |
(2.11) |
Bezpośrednio z wzoru 2.6 dostajemy (dla  )
)
Tak więc z wzoru 2.5
W sumie kosinusów wyrazy dla  znoszą odpowiednie wyrazy dla
znoszą odpowiednie wyrazy dla 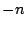 , w sumie
sinusów wyrazy dla
, w sumie
sinusów wyrazy dla 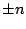 dodają się, dając w efekcie
dodają się, dając w efekcie
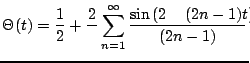 |
(2.12) |
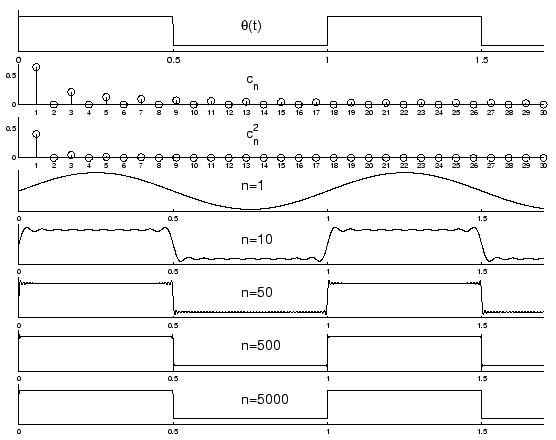
Rysunek:
Od góry, kolejno:
funkcja  (równanie 2.11), ,,uzupełniona'' do funkcji okresowej według wzoru
2.10, pierwszych 30 współczynników szeregu Fouriera,
kwadraty współczynników szeregu Fouriera -- dyskretne widmo,
pierwszy wyraz rozwinięcia Fouriera, sumy pierwszych 10, 50, 500 i 5000 wyrazów rozwinięcia
(2.12). Jak widać, najtrudniejsza do wyrażenia z pomocą funkcji
trygonometrycznych jest nieciągłość funkcji
(równanie 2.11), ,,uzupełniona'' do funkcji okresowej według wzoru
2.10, pierwszych 30 współczynników szeregu Fouriera,
kwadraty współczynników szeregu Fouriera -- dyskretne widmo,
pierwszy wyraz rozwinięcia Fouriera, sumy pierwszych 10, 50, 500 i 5000 wyrazów rozwinięcia
(2.12). Jak widać, najtrudniejsza do wyrażenia z pomocą funkcji
trygonometrycznych jest nieciągłość funkcji  w punktach
w punktach
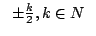 ; niejednorodna
zbieżność szeregów Fouriera w tych rejonach nosi nazwę efektu Gibbsa.
; niejednorodna
zbieżność szeregów Fouriera w tych rejonach nosi nazwę efektu Gibbsa.
|
|
![]() , określonego na skończonym przedziale
, określonego na skończonym przedziale ![]() ,
możemy utworzyć sygnał okresowy
,
możemy utworzyć sygnał okresowy ![]() :
:
![]() )
)
![$\displaystyle c_{n} = \frac{1}{T}\int_{0}^{T} \Theta(t) e^\frac{i 2\pi n t}{T} ...
...0 ) =
\left [\frac{1}{i 2\pi n} e^{{i 2\pi n t}} \right ]_{t=0}^{t=\frac{1}{2}}$](img162.png)