Falki (wavelets)

Falka to funkcja $\psi \in L^2(\mathbb{R})$ o zerowej średniej:

$$\int_{-\infty}^{\infty}\psi(t) dt = 0$$ (3.3)

Aby spełnić ten warunek, niezerowa funkcja musi oscylować, choć niekoniecznie (wręcz raczej nie) w sposób okresowy, jak ,,duże'' fale $e^{ikt}$--stąd nazwa.

Reprezentacja konstruowana jest ze ,,współczynników falkowych'' - iloczynów skalarnych sygnału ze znormalizowanymi ( $\Vert\psi\Vert=1$) funkcjami generowanymi jako przesunięcia i rozciągnięcia falki $\psi$:

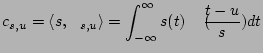$$c_{s,u} = \left<s, \psi_{s,u}\right> = \int_{-\infty}^{\infty} s(t) \psi(\frac{t-u}{s}) dt$$ (3.4)

Transformacja odwrotna istnieje, jeśli zbiór falek $\left\{\psi_i\right\}_{i\in I}$ tworzy ramę (ang. frame):

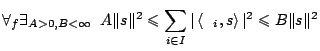$$\forall_f \exists_{A>0, B<\infty} \;\; A\Vert s\Vert^2 \le \sum_{i\in I} \vert\left<\psi_i, s\right>\vert^2 \le B\Vert s\Vert^2$$ (3.5)

Dopiero w latach 80. XX wieku udowodniono, że ze specjalnie dobranych falek można skonstruować ortogonalną bazę, jeśli kolejne skale $s$ będą tworzyły sekwencję diadyczną, czyli $s_n=2^ns_0$. Doprowadziło to do eksplozji zastosowań czasowo-częstościowych metod analizy sygnałów -- nie tylko ze względu na cenione przez fizyków własności baz ortogonalnych, jak zachowanie energii reprezentacji czy prosta formuła rekonstrukcji, ale głównie dzięki powstaniu szybkich algorytmów obliczeniowych.

Rysunek: Podział przestrzeni czas-częstość dla wielorozdzielczej analizy falkowej.