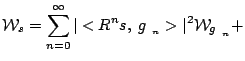 | |||
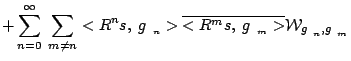 |
|||
Podwójna suma zawiera wyrazy mieszane, znacząco fałszujące obraz rozkładu
energii sygnału w klasycznej transformacie Wignera i pochodnych; minimalizacja
ich wkładu w tych rozkładach jest przedmiotem zastosowań zaawansowanych
technik matematycznych.
Dzięki rozkładowi sygnału postaci równania (4.6), możliwe
jest ich usunięcie explicite -- po prostu pomijamy podwójną sumę, definiując
wielkość
![]() :
:
Dystrybucja Wignera pojedynczego atomu ![]() spełnia
spełnia
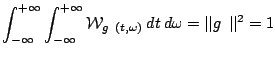 |
(4.11) |
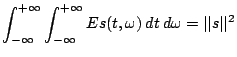 |
(4.12) |
Wynik działania algorytmu ze słownikiem funkcji Gabora przedstawia rysunek 4.1; sygnał zasymulowano jako sumę sinusa, delty Diraca (jednopunktowej nieciągłości) i trzech funkcji Gabora o parami jednakowych położeniach w czasie i częstościach. Rysunek 4.2 przedstawia dekompozycję tegoż sygnału z dodanym liniowo szumem o dwukrotnie większej energii.