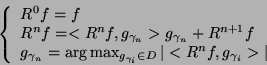 |
(1) |
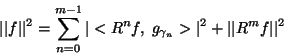 |
(2) |
Results of the above procedure depend on the set of functions
available for the decomposition, i.e. the dictionary.
We use Gabor functions
(sine-modulated Gaussian), which provide optimal joint time-frequency
localization. A real Gabor function can be expressed as:
However, within ranges of these continuous parameters no particular sampling is a priori defined, so we are confronted with a potentially infinite dictionary size. Therefore, in practical implementations, we use subsets of the possible dictionary functions. In choosing such subset, any fixed subsampling of the parameter space introduces a statistical bias in the resulting parametrization. Free of bias parametrization is possible with stochastic dictionaries, where the parameters of a dictionary's atoms are randomized before each decomposition. Further details can be found in [3].
In general, mathematics related to the non-linear MP algorithm can be
quite complicated. Nevertheless, for a reasonable application if its
results, it is basically enough to understand that structures present
in the signal are explained in terms of functions ![]() (equation (3)), chosen for its representation from
the dictionary. In case of the Gabor dictionary, each of these
structures will be described by it's time and frequency positions,
time spread, amplitude and phase.
(equation (3)), chosen for its representation from
the dictionary. In case of the Gabor dictionary, each of these
structures will be described by it's time and frequency positions,
time spread, amplitude and phase.