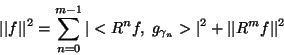

Next: Discrete Gabor dictionary
Up: Introduction
Previous: Introduction
Matching pursuit
Given a set of functions (dictionary)
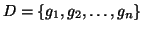 such that
such that 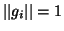 , we can define an
optimal
, we can define an
optimal 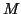 -approximation as an expansion, minimizing the error
-approximation as an expansion, minimizing the error 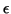 of an approximation
of signal
of an approximation
of signal 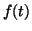 by
by 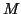 waveforms:
waveforms:
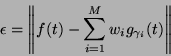 |
(1) |
where
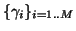 represents the indices of the chosen functions
represents the indices of the chosen functions 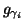 .
Finding such an optimal approximation is an NP-hard problem [5].
A suboptimal expansion can be found by means of an iterative procedure, such as the matching pursuit
algorithm (MP).
.
Finding such an optimal approximation is an NP-hard problem [5].
A suboptimal expansion can be found by means of an iterative procedure, such as the matching pursuit
algorithm (MP).
In the first step of MP, the waveform 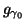 which best matches the signal
which best matches the signal 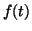 is chosen.
In each of the consecutive steps, the waveform
is chosen.
In each of the consecutive steps, the waveform 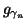 is matched to the signal
is matched to the signal  ,
which is the residual left after subtracting results of previous iterations:
,
which is the residual left after subtracting results of previous iterations:
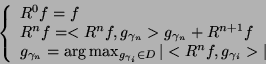 |
(2) |
Orthogonality of 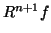 and
and 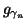 in each step implies energy conservation:
in each step implies energy conservation:
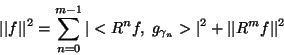 |
(3) |
For a complete dictionary the procedure converges to 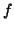 :
:
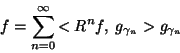 |
(4) |
From this equation we can derive a time-frequency distribution
of the signal's energy, that is free of cross-terms, by adding Wigner distributions of selected functions:
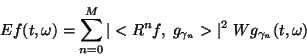 |
(5) |


Next: Discrete Gabor dictionary
Up: Introduction
Previous: Introduction
Piotr J. Durka
2001-03-23
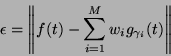
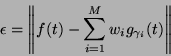
![]() which best matches the signal
which best matches the signal ![]() is chosen.
In each of the consecutive steps, the waveform
is chosen.
In each of the consecutive steps, the waveform ![]() is matched to the signal
is matched to the signal ![]() ,
which is the residual left after subtracting results of previous iterations:
,
which is the residual left after subtracting results of previous iterations: