

Next: Matching Pursuit with stochastic
Up: Introduction
Previous: Matching pursuit
Discrete Gabor dictionary
Gabor functions (sine-modulated Gaussian functions) provide optimal joint time-frequency localization.
A real Gabor function can be expressed as:
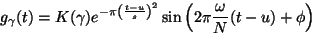 |
(6) |
N is the size of the signal for which the dictionary is constructed, 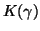 is such that
is such that
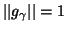 .
.
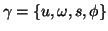 denotes parameters of the
dictionary's functions (time-frequency atoms).
The length of signal (
denotes parameters of the
dictionary's functions (time-frequency atoms).
The length of signal (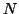 points)
suggests ranges for the parameters of Gabor functions which can be reasonably fitted to such an epoch.
However, within these ranges no particular
sampling is a priori defined, and we are confronted with a three-dimensional
points)
suggests ranges for the parameters of Gabor functions which can be reasonably fitted to such an epoch.
However, within these ranges no particular
sampling is a priori defined, and we are confronted with a three-dimensional![[*]](footnote.png) continuous space; this results in an infinite dictionary size.
Therefore, in practical implementations, we use subsets of the possible dictionary functions.
continuous space; this results in an infinite dictionary size.
Therefore, in practical implementations, we use subsets of the possible dictionary functions.
In the dictionary implemented originally by Mallat and Zhang in [1], the parameters of the atoms are
chosen from dyadic sequences of integers.
Their sampling is governed by an extra parameter--octave 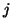 (integer). Scale
(integer). Scale 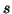 , which corresponds
to an atom's width in time, is derived from the dyadic sequence
, which corresponds
to an atom's width in time, is derived from the dyadic sequence
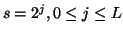 (signal size
(signal size 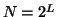 ).
Parameters
).
Parameters 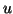 and
and 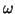 , which correspond to an
atom's position in time and frequency, are sampled for each octave
, which correspond to an
atom's position in time and frequency, are sampled for each octave 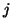 with interval
with interval 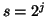 , or,
if oversampling by
, or,
if oversampling by 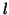 is introduced, with interval
is introduced, with interval 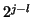 .
.
Footnotes
- ... three-dimensional
![[*]](footnote.png)
- The phase
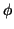 is usually optimized in each step of the MP procedure separately for each fitted atom.
is usually optimized in each step of the MP procedure separately for each fitted atom.


Next: Matching Pursuit with stochastic
Up: Introduction
Previous: Matching pursuit
Piotr J. Durka
2001-03-23
![[*]](footnote.png) continuous space; this results in an infinite dictionary size.
Therefore, in practical implementations, we use subsets of the possible dictionary functions.
continuous space; this results in an infinite dictionary size.
Therefore, in practical implementations, we use subsets of the possible dictionary functions.
![]() (integer). Scale
(integer). Scale ![]() , which corresponds
to an atom's width in time, is derived from the dyadic sequence
, which corresponds
to an atom's width in time, is derived from the dyadic sequence
![]() (signal size
(signal size ![]() ).
Parameters
).
Parameters ![]() and
and ![]() , which correspond to an
atom's position in time and frequency, are sampled for each octave
, which correspond to an
atom's position in time and frequency, are sampled for each octave ![]() with interval
with interval ![]() , or,
if oversampling by
, or,
if oversampling by ![]() is introduced, with interval
is introduced, with interval ![]() .
.
![[*]](footnote.png)