Introduction

EEG (electroencephalogram) reflects electrical activity of a multitude of neural populations in the brain. This signal is extremely complex, since EEG is generated as a superposition of different simultaneously acting dynamical systems. The oscillatory activity of neuronal pools reflected in characteristic EEG rhythms constitutes a mechanism by which the brain can regulate changes of state in selected neuronal networks to cause a qualitative transitions between modes of information processing [Lopes Da Silva, 1996].

The complex character of EEG and its significance in brain research and clinical practice brought early introduction of signal analysis methods to EEG studies. Spectral methods of EEG processing can be traced back to the first attempt of Fourier analysis application to EEG in 1932 [Dietsch, 1932]. Fast Fourier transform (FFT) was applied to EEG soon after its introduction, and until today spectral analysis remains the most widespread signal processing method in this field. Limitations of FFT promoted introduction of parametric methods such as autoregressive (AR) or autoregressive - moving average (ARMA) models, free from the windowing effects.

Development of non-linear methods of signal analysis brought explosion of works concerning application of chaotic formalism to EEG [Basar and Bullock, 1989] [Dvorák and Holden, 1991]. Works of Freeman, based on carefully planned physiological experiments, brought new insights into the mechanisms of non-linear modes of brain operation [Skarda and Freeman, 1987]. However, tracing of chaos in EEG proved to be more difficult than it was expected. It has been shown, that linear forecasting of signals from human and animal brains is as good--and sometimes better--as the non-linear prediction [Blinowska and Malinowski, 1991]. Tests of non-linear procedures, performed on surrogate (phase disturbed) data, revealed their failure in description of different kinds of EEG time series [Achermann et al., 1994] [Pijn et al., 1991].

In view of the presently available evidence, application of typical methods of non-linear time series analysis, such as calculation of attractor dimension or Ljapunov coefficients, seems to be fully justified only for special cases such as e.g. epileptic EEG [Pijn et al., 1991] or activity of a group of neurons in a well defined operation mode [Skarda and Freeman, 1987]. This fact it is not surprising when we consider the multitude of dynamic processes running in brain and their ever-changing character.

All the above mentioned methods, linear and non-linear, assume stationarity of the signal--in spite of the fact, that information processing by brain is mostly reflected in fast dynamic changes of its activity. This fact implies the application to the analysis of EEG and LFP (locald field potentials) methods operating in time-frequency space.

First method which allowed for the time-frequency representation of signal's energy distribution was windowed Fourier transform (WFT). It relies on on estimation of power spectra (by Fourier transform) for short time windows, shifted along the time axis.

Widespread application of time-frequency methods of signal analysis started in eighties with the Wavelet Transform (WT), which offers signal's description in terms of coefficients {$c_{s,u}$} representing signal's energy content in a specified time-frequency region. This representation is constructed by means of decomposition of the signal $f$ over a set of waveforms generated by translating ($u$) and scaling ($s$) one function--wavelet $\psi$, possibly well concentrated in time and frequency:

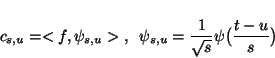$$c_{s,u}= <f, \psi_{s,u} > \;, \;\; \psi_{s,u} ={ 1 \over {\sqrt{s}} }\psi \bigl( {{t-u} \over {s}} \bigr)$$ (1)

Linear decomposition of signal in a wavelet basis was a significant improvement over the windowed Fourier transform (WFT), allowing for orthogonal representation, fast numerical implementations and multiresolution decomposition of signals [Mallat, 1989]. WT is being successfully applied e.g. for analysis of time-locked EEG phenomena (evoked potentials), where it's main drawback--sensitivity of the representation to the time shift of analyzed window [Durka, 1996]--is not essential. However, neither WT nor WFT provide enough resolution and flexibility in a general case, like description of transients occurring more or less randomly in time.

High resolution time-frequency representation of signal's energy can be constructed by Cohen's class transforms [Williams, 1997]; they all derive from the quadratic Wigner transform which can be expressed as:

$$W_f(t, \omega)=\int f \bigl (t + {\tau \over 2\;} \bigr)\; \... ...bigl(t- {\tau \over 2} \bigr )\; } e^{- i \omega \tau } d \tau$$ (2)

This representation satisfies the time and frequency marginals, but contains severe cross terms between different time-frequency structures, which may lead to misinterpretation. Sophisticated mathematics applied to reduce this effect created class of Reduced Interference Distributions (see e.g. [Williams, 1997]), where reduction of cross terms is usually achieved at the cost of marginal properties.

In spite of high resolution offered by Cohen's class transforms, their application is practically limited to visual inspection of time-frequency plots for each analyzed data epoch. The method, which allows for parametric--fully quantitative--description of signals in time-frequency space is the Matching Pursuit (MP), a method based on adaptive approximation of time series by functions chosen for each analyzed epoch. The MP was introduced by Mallat and Zhang (1993). The first application to biological signal concerned EEG analysis [Durka and Blinowska, 1995]. In the following we shall describe the MP method itself, then we shall point out some of the limitations of the original approach, and finally we shall present the way of overcoming the bias of the original method. Properties of MP parametrization will be demonstrated on the example of sleep EEG, however the method is suitable for all kinds of signals, in particular non-stationary time series.