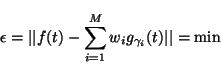

Next: Matching Pursuit algorithm
Up: Unbiased high resolution method
Previous: Introduction
The method relies on the approximation of the signal by functions
(time-frequency atoms) chosen from a very large and redundant
set. Given a set of functions (dictionary)
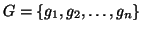 such that
such that 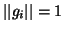 , we can define an optimal
, we can define an optimal 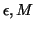 -approximation as an expansion minimizing the error
-approximation as an expansion minimizing the error 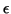 of
the approximation of signal
of
the approximation of signal 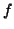 by
by 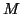 atoms. Such an expansion is
defined by the set of indices
atoms. Such an expansion is
defined by the set of indices
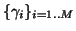 of the chosen
functions
of the chosen
functions 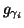 and their weights
and their weights 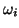 :
:
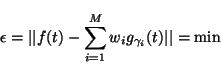 |
(3) |
Finding such an optimal
approximation is a NP-hard problem [Davis, 1994]. Another problem
emerges from the fact that such an expansion would be unstable with
respect to the number 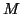 of used waveforms: changing
of used waveforms: changing 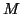 even by one
can completely change the set of waveforms chosen for the
representation. These problems turn our attention to sub-optimal
solutions. A sub-optimal expansion, stable with respect to the number
of chosen waveforms, can be found by means of an iterative procedure,
such as the Matching Pursuit algorithm proposed by Mallat and Zhang
[Mallat and Zhang, 1993] (similar approach was discussed by Qian et
al. [Qian et al., 1992]).
even by one
can completely change the set of waveforms chosen for the
representation. These problems turn our attention to sub-optimal
solutions. A sub-optimal expansion, stable with respect to the number
of chosen waveforms, can be found by means of an iterative procedure,
such as the Matching Pursuit algorithm proposed by Mallat and Zhang
[Mallat and Zhang, 1993] (similar approach was discussed by Qian et
al. [Qian et al., 1992]).
Subsections


Next: Matching Pursuit algorithm
Up: Unbiased high resolution method
Previous: Introduction
Piotr J. Durka
2001-06-11