

Next: Sleep spindles detection and
Up: The method
Previous: Time-frequency energy distribution
In Figure 1a a simple signal is constructed
from continuous sine wave (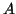 ), one-point discontinuity (Dirac's
delta,
), one-point discontinuity (Dirac's
delta, 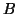 ) and three Gabor functions (
) and three Gabor functions (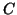 ,
, 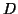 and
and 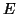 ) of the same
time positions (
) of the same
time positions (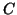 and
and 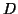 ) or the same frequencies (
) or the same frequencies (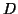 and
and 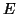 ).
Figure 1b gives time-frequency energy
distribution obtained for this signal from MP decomposition by means
of eq. (12). In the left, 3-dimensional plot, energy is
proportional to the height. Right 2-dimensional plot presents energy
in shades of gray. Perfect representation of all the signal
structures is due to the fact that the signal was constructed as a
sum of dictionary's elements only.
).
Figure 1b gives time-frequency energy
distribution obtained for this signal from MP decomposition by means
of eq. (12). In the left, 3-dimensional plot, energy is
proportional to the height. Right 2-dimensional plot presents energy
in shades of gray. Perfect representation of all the signal
structures is due to the fact that the signal was constructed as a
sum of dictionary's elements only.
Figure 1:
(a): left--components of the simulated signal: sine
A, Dirac's delta B and Gabor functions C,
D and E. Right--signals, labelled b, c and
d, constructed as sum of structures A-E and white noise,
and decomposed in corresponding panels (b), (c) and (d). (b): time-frequency energy distribution
(eq. 12) obtained for sum of structures A-E; in 3-D
representation on the left energy is proportional to the height, in
right panel--to the shades of gray. Panels (c) and
(d): decompositions of signals with linear addition of noise,
S/N = 1/2 (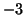 dB) in (c) and
dB) in (c) and 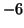 dB in (d), the same
realization of white noise was used in both cases. Exact parameters
of presented time-frequency structures are given in
Table 1.
dB in (d), the same
realization of white noise was used in both cases. Exact parameters
of presented time-frequency structures are given in
Table 1.
![\includegraphics[width=\columnwidth]{figures/fig01.eps}](img60.png) |
In Figure 1c and 1d
a white noise of energy twice and four times the signal's energy is
added. In both cases the same realization of white noise was used
(with different weights). Table 1 presents parameters
of simulated time-frequency structures 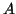 -
-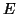 compared to parameters
of corresponding time-frequency atoms fitted by MP to the mentioned
signals, with S/N ratio from
compared to parameters
of corresponding time-frequency atoms fitted by MP to the mentioned
signals, with S/N ratio from 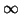 (simulated signal
(simulated signal 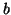 without
noise) through 1/2 (
without
noise) through 1/2 (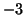 dB, signal c) to 1/4 (
dB, signal c) to 1/4 (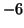 dB, signal
d).
dB, signal
d).
We can observe some characteristic properties of decomposition:
- Sine wave
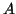 retains its frequency up to the noisiest signal,
however, even in the absence of noise additional shorter structures
are fitted near the beginning and the end of the signal to account for
border effects. In noisy signal the 'infinite' sine tends to be
explained by two shorter structures, due to border effects again.
retains its frequency up to the noisiest signal,
however, even in the absence of noise additional shorter structures
are fitted near the beginning and the end of the signal to account for
border effects. In noisy signal the 'infinite' sine tends to be
explained by two shorter structures, due to border effects again.
- Dirac's delta disappears in the strongest noise, but till then
preserves its exact time position.
- Gabor function
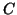 , being the only structure in this frequency,
retains relatively well all of the parameters with a slight flow of
time position at higher noise levels.
, being the only structure in this frequency,
retains relatively well all of the parameters with a slight flow of
time position at higher noise levels.
- Finally, the two Gabor functions
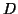 and
and 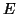 lying in the same
frequency with different time positions and widths exhibit slight flow
of parameters for S/N=1/2, and in higher noise melt in two longer
structures: one in between (in Table 1 assigned to
structure
lying in the same
frequency with different time positions and widths exhibit slight flow
of parameters for S/N=1/2, and in higher noise melt in two longer
structures: one in between (in Table 1 assigned to
structure 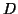 ) and one more to the right.
) and one more to the right.
The above example demonstrates robustnes of the method in
presence of linearly added white noise--in this case most of the
basic time-frequency characteristics were represented even in S/N=1/4
(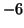 dB).
dB).


Next: Sleep spindles detection and
Up: The method
Previous: Time-frequency energy distribution
Piotr J. Durka
2001-06-11
![\includegraphics[width=\columnwidth]{figures/fig01.eps}](img60.png)
![\includegraphics[width=\columnwidth]{figures/fig01.eps}](img60.png)
![]() -
-![]() compared to parameters
of corresponding time-frequency atoms fitted by MP to the mentioned
signals, with S/N ratio from
compared to parameters
of corresponding time-frequency atoms fitted by MP to the mentioned
signals, with S/N ratio from ![]() (simulated signal
(simulated signal ![]() without
noise) through 1/2 (
without
noise) through 1/2 (![]() dB, signal c) to 1/4 (
dB, signal c) to 1/4 (![]() dB, signal
d).
dB, signal
d).