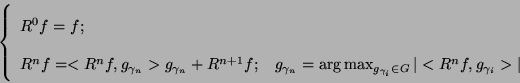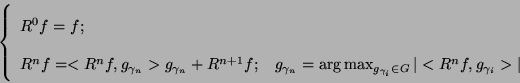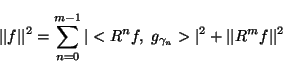

Next: Discrete dyadic Gabor dictionary
Up: The method
Previous: The method
MP (introduced in [Mallat and Zhang, 1993]) is an iterative, non-linear
procedure which decomposes signal into a linear expansion of waveforms
chosen from a redundant dictionary. In the first step, waveform
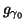 matching best the signal
matching best the signal 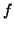 is chosen, and in each of
consecutive steps waveform
is chosen, and in each of
consecutive steps waveform 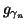 is matched to signal's
residuum
is matched to signal's
residuum 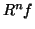 , left after subtracting results of previous
iterations:
, left after subtracting results of previous
iterations:
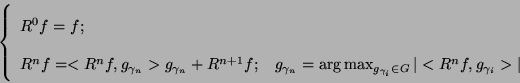 |
(4) |
Orthogonality of 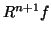 and
and 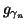 in each step implies
energy conservation:
in each step implies
energy conservation:
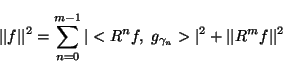 |
(5) |
If the dictionary is complete, which is usually the case, the
procedure converges to 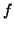 , i.e.
, i.e.
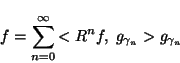 |
(6) |
Piotr J. Durka
2001-06-11