The HFB approximation is based on the use of a trial variational
wave function which is assumed to be an independent quasiparticle
state
![]() . This state, which mixes different
eigenstates of the particle number operator, is a linear combination
of independent particle states representing various possibilities of
occupying pairs of single particle states.
Following the notations and phase convention of [5]
we define the particle and pairing density
. This state, which mixes different
eigenstates of the particle number operator, is a linear combination
of independent particle states representing various possibilities of
occupying pairs of single particle states.
Following the notations and phase convention of [5]
we define the particle and pairing density ![]() and
and
![]() matrices by
matrices by
| (1) |
| (2) |
The variation of the energy expectation value
![]() with respect to
with respect to ![]() and
and
![]() under the constraints
under the constraints
![]() and
and
![]() (for neutrons and protons)
leads to the Hartree-Fock-Bogolyubov equation which reads
in coordinate representation
(for neutrons and protons)
leads to the Hartree-Fock-Bogolyubov equation which reads
in coordinate representation
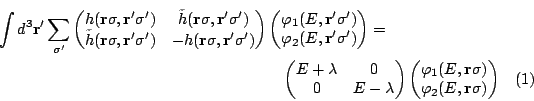
 |
(3) |