The 0
In addition to the spurious state associated with nonconservation of particle-number by the HFB, the ![]() channel contains the important ``breathing mode''.
In Table 1 we display results from a run with
channel contains the important ``breathing mode''.
In Table 1 we display results from a run with
![]() =
=![]() for neutrons and
for neutrons and
![]() MeV for protons,
resulting in the inclusion of 310 proton quasiparticle states and the same number of
neutron states, with angular momentum up to
MeV for protons,
resulting in the inclusion of 310 proton quasiparticle states and the same number of
neutron states, with angular momentum up to ![]() .
The Table shows the QRPA energies and transition matrix elements of the
particle-number operator. The spurious state is below 200 keV, well separated from the other states, all of which have negligible ``number-strength''. The nonzero number strength in the
spurious state, like the nonzero energy of that state, is a measure of
numerical error.
If the space of two-quasiparticle states is smaller, with
.
The Table shows the QRPA energies and transition matrix elements of the
particle-number operator. The spurious state is below 200 keV, well separated from the other states, all of which have negligible ``number-strength''. The nonzero number strength in the
spurious state, like the nonzero energy of that state, is a measure of
numerical error.
If the space of two-quasiparticle states is smaller, with
![]() MeV and
MeV and
![]() , the energy of the spurious state
and the number strength barely change.
, the energy of the spurious state
and the number strength barely change.
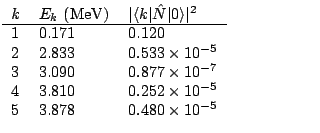 |
![\includegraphics[width=12cm]{174Sn0cutoff}](img71.png) |
Figure 2 shows the strength function
![]() for the isoscalar
for the isoscalar ![]() transition operator, cf. [75],
transition operator, cf. [75],
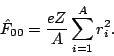 |
(3) |
The dependence of the strength function on the box size and
quasiparticle cutoff is shown in
Fig. 3. The upper part of the Figure
(panels a-c) corresponds
to a constant smoothing width of ![]() =0.5 MeV. This relatively
small value is not sufficient to eliminate the finite-box effects
but it allows us to assess the stability of the QRPA solutions
as a function of
=0.5 MeV. This relatively
small value is not sufficient to eliminate the finite-box effects
but it allows us to assess the stability of the QRPA solutions
as a function of ![]() .
The large structure corresponding to the giant monopole resonance (GMR)
is independent of box size no matter what the cutoff, but increasing the number of configurations magnifies the dependence on box size of local fluctuations in
.
The large structure corresponding to the giant monopole resonance (GMR)
is independent of box size no matter what the cutoff, but increasing the number of configurations magnifies the dependence on box size of local fluctuations in ![]() .
The lower part of the Figure (panels d-f) are smoothed more realistically, as in
Eq. (2). It is gratifying to see
that the resulting strength functions are practically identical,
i.e., the remaining dependence on
.
The lower part of the Figure (panels d-f) are smoothed more realistically, as in
Eq. (2). It is gratifying to see
that the resulting strength functions are practically identical,
i.e., the remaining dependence on ![]() and the cutoff is very weak.
and the cutoff is very weak.
![\includegraphics[width=15cm]{174Snbox0}](img74.png) |
The energy-weighted sum rule (EWSR) for the isoscalar ![]() mode [75] is given by
mode [75] is given by