The isoscalar 1
The ![]() channel, home of the giant dipole resonance, the isoscalar squeezing
resonance, and as yet incompletely understood low-energy peaks in neutron-rich
nuclei (sometimes associated with skin excitations),
has a spurious isoscalar mode associated with center-of-mass motion that
can seriously compromise the low-energy spectrum if not handled with extreme
care. We test the ability of our QRPA to do so in
channel, home of the giant dipole resonance, the isoscalar squeezing
resonance, and as yet incompletely understood low-energy peaks in neutron-rich
nuclei (sometimes associated with skin excitations),
has a spurious isoscalar mode associated with center-of-mass motion that
can seriously compromise the low-energy spectrum if not handled with extreme
care. We test the ability of our QRPA to do so in
![]() Sn,
Sn, ![]() Sn,
Sn, ![]() Sn, and
Sn, and ![]() Sn.
(The nuclei
Sn.
(The nuclei ![]() Sn and
Sn and ![]() Sn are the
two-proton and two-neutron drip-line systems predicted by the HFB calculation
with SkM
Sn are the
two-proton and two-neutron drip-line systems predicted by the HFB calculation
with SkM![]() . Neither nucleus has any static pairing,
i.e.,
. Neither nucleus has any static pairing,
i.e.,
![]() =
=
![]() =0.) In the following calculations, we take
=0.) In the following calculations, we take
![]() MeV for the protons and
MeV for the protons and
![]() for
the neutrons. As discussed above, smoothed strength
functions are practically independent of small changes in the cutoff.
They are also independent of the cutoff in quasiparticle angular momentum
provided we include all states with
for
the neutrons. As discussed above, smoothed strength
functions are practically independent of small changes in the cutoff.
They are also independent of the cutoff in quasiparticle angular momentum
provided we include all states with ![]()
![]() 15/2.
15/2.
Figure 4 shows the
predicted isoscalar dipole strength
function for
![]() Sn.
Sn.
![\includegraphics[width=13cm]{100176Sn}](img89.png) |
We display the fine structure of the isoscalar ![]() strength functions in
strength functions in ![]() Sn and
Sn and ![]() Sn in Fig. 5, which also illustrates
the dependence of the results on
Sn in Fig. 5, which also illustrates
the dependence of the results on ![]() . The dependence is consistent
with that of Fig. 3 for the isoscalar 0
. The dependence is consistent
with that of Fig. 3 for the isoscalar 0![]() strength;
the low-amplitude fluctuations in
strength;
the low-amplitude fluctuations in ![]() that are unstable as a function of
that are unstable as a function of ![]() disappear, and the smoothed strength function depends only weakly
on
disappear, and the smoothed strength function depends only weakly
on ![]() . In
. In ![]() Sn, the two sharp peaks below
10 MeV correspond to discrete states while the broad maxima centered
around 15 MeV and 27 MeV are in the continuum, well above
neutron-emission threshold. A similar three-peaked structure
emerges in
Sn, the two sharp peaks below
10 MeV correspond to discrete states while the broad maxima centered
around 15 MeV and 27 MeV are in the continuum, well above
neutron-emission threshold. A similar three-peaked structure
emerges in ![]() Sn,
though most of the strength there is concentrated in the low-energy peak
at
Sn,
though most of the strength there is concentrated in the low-energy peak
at ![]() MeV. Fig. 4 shows (as we will discuss
in our forthcoming paper [76]) that the appearance of
the low-energy isoscalar dipole strength is a real and dramatic feature
of neutron-rich dripline nuclei [77,78].
MeV. Fig. 4 shows (as we will discuss
in our forthcoming paper [76]) that the appearance of
the low-energy isoscalar dipole strength is a real and dramatic feature
of neutron-rich dripline nuclei [77,78].
![\includegraphics[width=15cm]{174Snbox1}](img94.png) |
The EWSR for the isoscalar ![]() mode [75] is
mode [75] is
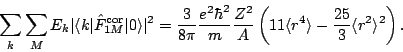 |
(7) |