Diabatic blocking

Crossing or non-crossing (``repulsion") of the mean-field single-particle energy levels in function of some continuous parameter(s) of theory, such as the rotational frequency and/or the constraining multipole moments, is one of the most important phenomena in the studies of high-spin nuclear states. They may give rise to several kinds of characteristic irregularities occurring along the rotational bands and these irregularities often help significantly in assigning the theoretical single-particle configurations to the experimental rotational bands.

As it is well known, levels that differ in terms of their discrete good quantum numbers such as, for instance, simplex, parity, signature ... etc., will generally cross. These crossings are such that the underlying intrinsic characteristics (e.g. single-particle alignments or multipole moments) do not change in any remarkable way before and after the crossing and this mechanism will be of no interest here.

In contrast, levels that belong to the same discrete symmetry will most of the time approach each other in function of the parameter studied and then go apart but in such a way that the intrinsic characteristics of the first one will go over to the second one and vice versa. This non-crossing rule, sometimes called the Landau-Zener effect, cannot be given any more rigorous general formulation, and it may happen that the distance of the closest approach for the same symmetry levels is zero. In those, in practice very rare cases, the two crossing mechanisms mentioned do not differ.

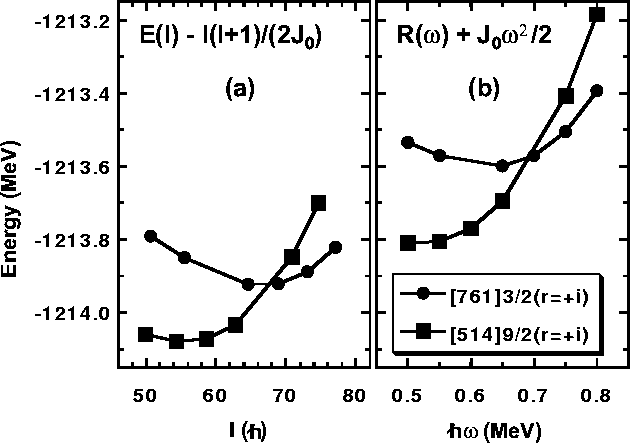
An example of a crossing of two HF configurations (no pairing) is presented in Fig. 1. The left panel shows the total energies E(I) as functions of the total spin I, while the right panel shows the total Routhians $R(\omega )$=$E(\omega)$- $I(\omega)\omega$ as functions of the rotational frequency ${\hbar\omega}$. Since both quantities vary very rapidly as functions of their arguments, they are plotted with respect to the corresponding rigid-rotor reference values, i.e., E(I) is shown relatively to I(I+1)/(2J₀), and $R(\omega )$ is shown relatively to $-J_0\omega^2/2$, where the constant rigid-rotor moment of inertia of J₀=100$\hbar^2$/MeV has been used. Calculations have been performed within the cranking approximation for values of the rotational frequency of ${\hbar\omega}$=0.5(0.05)0.8MeV.

The examples shown in Fig. 1 correspond to two bands in ¹⁵¹Tb (see Ref. [6] for a more complete description of calculations performed in this nucleus). Both configurations contain the same set of the single-particle levels of ¹⁵⁰Tb being occupied. They correspond to the neutron and proton configurations of ( N₊₊,N_+-,N_-+,N_-)=(22,21,21,21) and (15,16,17,17), respectively, as described by the numbers of states occupied in the parity-signature blocks ($\pi$,r)=(+1,+i), (+1,-i), (-1,+i), and ( -1,-i). The ground-state band in ¹⁵¹Tb can be obtained by putting the 86th neutron into the lowest available level for N_+-=22, thus obtaining the closed N=86 SD magic neutron configuration. Since the order of orbitals may change with changing rotational frequency, numbers $N_{\pi,{-ir}}$ are not necessarily the most practical for defining physical characteristics of the single-particle states in question. Usually, one uses the so-called asymptotic Nilsson quantum numbers $[Nn_z\Lambda]\Omega$[5] for that purpose. Code HFODD calculates these quantum numbers by finding the dominant Nilsson components of the HF single-particle states. Several excited bands in ¹⁵¹Tb can be obtained by putting the 86th neutron into one of the higher available levels, for instance, in the N_-+=22, 23, or 24 levels, that correspond to one of the [521]3/2(r=+i), [514]9/2(r=+i), or [761]3/2(r=+i) Nilsson orbitals.

  

Figure: Total energies E(I), (a), and total Routhians $R(\omega )$, (b), of the [761]3/2(r=+i) and [514]9/2(r=+i) neutron diabatic configurations in ¹⁵¹Tb. The rigid-rotor reference energies for J₀=100$\hbar^2$/MeV have been subtracted. (In our graphical representation we employ the convention according to which the levels that carry the smoothly varying intrinsic characteristics (see text) are denoted with the same symbols. This is at variance with the convention that stresses the Landau-Zener mechanism, as used by some authors. According to the latter one, the sequences of the lowest-lying points would have been drawn as squares and that of the higher-lying points as circles.)

Of particular interest in ¹⁵¹Tb are exited bands in which the [761]3/2(r=+i) intruder orbital is occupied. This orbital decreases in energy with increasing rotational frequency, and therefore, it crosses the other ($\pi$,r)= (-1,+i) orbitals. In particular, in ¹⁵¹Tb the [761]3/2(r=+i) orbital corresponds to the N_-+=24th orbital at low frequencies, then it becomes the N_-+=23rd orbital, and finally, at high frequencies it is the lowest available N_-+=22nd orbital. Configurations shown in Fig. 1 correspond to the crossing of the [761]3/2(r=+i) and [514]9/2(r=+i) orbitals. Following the standard convention, these configurations are called the diabatic ones, because they correspond to the given orbital being occupied, irrespective of its excitation energy. On the other hand, configurations based on occupying the N_-+=22, 23, or 24 states are called the adiabatic ones. Obviously, in adiabatic configurations, different Nilsson orbitals are occupied at different frequencies.

Fig. 2 shows the negative-parity single-particle neutron Routhians in ¹⁵¹Tb. The left and right panels show the results obtained for the [761]3/2(r=+i) and [514]9/2(r=+i) diabatic configurations, respectively. The occupied orbitals are in both cases denoted by the filled symbols. It is clear that the crossing frequency depends on which of the shown orbitals is occupied. This is due to the self-consistent effects that influence the deformations, spins, and other characteristics of many-body states, calculated at given rotational frequencies and for given particle-hole configurations.

  

Figure 2: Negative-parity neutron single-particle Routhians in ¹⁵¹Tb calculated for the [761]3/2(r=+i) (a) and [514]9/2(r=+i) (b) neutron diabatic configurations. Solid and dashed curves denote the r=+i and r=-i signatures, respectively. The arrows denote the angular frequencies where the converged solutions near the crossing points could not be found.

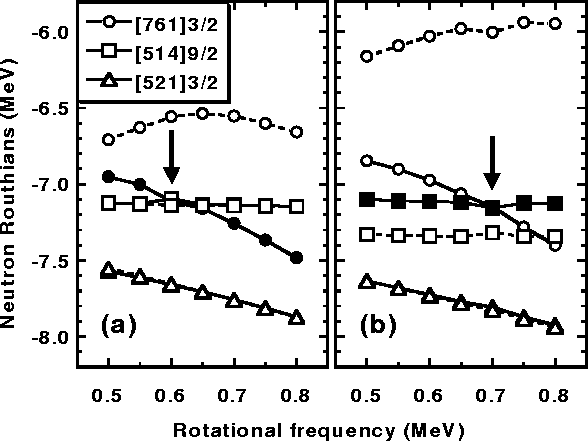In the calculations, one has to begin the analysis by finding the adiabatic configurations, in order to find the lowest available orbitals, to determine their physical characteristics, and to check whether or not there are any crossings of configurations that should be followed diabatically. The input data files tb151-a.dat and tb151-b.dat give examples of runs that find the adiabatic configurations for the N_-+=23rd and N_-+=24th orbitals being occupied, respectively.

After several HF iterations, the levels of the same symmetry, that are energetically sufficiently far, change their intrinsic characteristics (such as, e.g., angular momentum alignments) only by very small amounts. This is not true for the case of the crossing when the two states in question exchange their relative positions from one iteration to another. Therefore, in the HF calculations, very often the Landau-Zener avoided crossings of levels manifest themselves in the form of diverging iteration procedure. This observation is used by the code HFODD (v1.75r) in order to locate the crossing by recognizing the oscillatory (``ping-pong'') behavior of solutions.

  

Table 1: Example of the output printed when the ``ping-pong'' divergence is found, see text.

The ``ping-pong'' divergence is a result of the standard self-consistent prescription, for which the occupied states in a given iteration are the eigenstates of the mean-field Hamiltonian diagonalized in the preceding iteration. Such a divergence is characterized by two series of HF states, each one appearing in every second HF iteration. Focusing our attention on the specific example discussed above, one can describe such a divergence in the following way. Suppose that in a given HF iteration, the single-particle orbital [761]3/2(r=+i) appears below the [514]9/2(r=+i) orbital, i.e., it corresponds to N_-+=23. In this particular iteration it becomes occupied, and is included in all densities, for which the mean-field Hamiltonian is determined. In the next iteration, the new Hamiltonian is diagonalized, however, at present the orbital [514]9/2(r=+i) appears below [761]3/2(r=+i), and it is this orbital, again for N_-+=23, which becomes occupied. It is obvious that such a situation may repeat itself infinitely many times, never leading to a self-consistent solution.

In many cases, it is possible to find converged solutions near the crossing points simply by decreasing the convergence rate, i.e., by using parameters SLOWEV and SLOWOD (see Sec. 3.5 of II) only slightly smaller then 1. This method works well provided that the two crossing orbitals have fairly different characteristics, like it is the case in the example discussed here. However, in the case of a strong mixing between the two crossing orbitals, the HF iteration procedure converges near the crossing points only seldomly.

Upon recognizing the ``ping-pong'' divergence condition (see Sec. 3.1 for details of the procedure), the code HFODD (v1.75r) prints the summary table that may help in identifying the crossing orbitals. For the N_-+=23 adiabatic configuration at ${\hbar\omega}$=0.65MeV, the table has the form presented in Table 1.

In the upper part of the table, the code prints the absolute values of differences $\vert\Delta{}i_y\vert$ ( $\vert\Delta{}s_y\vert$) of single-particle average alignments i_y (intrinsic spins s_y) between the last and the last but one iterations (columns denoted by VALUE). The results are printed separately for the particle (empty) and hole (occupied) states, and their indices are given in columns denoted by INDEX. In each of the charge-parity-signature (or charge-simplex) blocks the results are printed only for those states for which the values of $\vert\Delta{}i_y\vert$ and $\vert\Delta{}s_y\vert$are the largest ones.

In the lower part of the table, the code prints the list of particle-hole pairs from the upper part of the table, for which the indices (INDEX) differ by one, i.e., which correspond to the particle-hole pairs at the Fermi surface. In the specific example discussed here, the code properly identifies the crossing of the N_-+=23 and N_-+=24 orbitals, and proposes the diabatic blocking based on the average values of the single-particle alignments, see Sec. 3.2. The crossing orbitals, [761]3/2(r=+i) and [514]9/2(r=+i), have markedly different alignments of about i_y=+2.23 and -0.46$\hbar$, respectively. This corresponds to values of $\vert\Delta{}i_y\vert$=+2.820 or 2.807$\hbar$printed in the table. Therefore, by requesting that the state that has a larger alignment be occupied (among the N_-+=23 and N_-+=24 orbitals), one obtains the diabatic [761]3/2(r=+i) configuration. Similarly, by choosing the state that has a smaller alignment, one obtains the [514]9/2(r=+i) diabatic configuration, and this is so irrespective of which orbital has smaller or larger energy, i.e., irrespective of the angular frequency. The input data files tb151-c.dat and tb151-d.dat give examples of runs that find the diabatic configurations for the [761]3/2(r=+i) and [514]9/2(r=+i) orbitals being occupied, respectively.