Example application

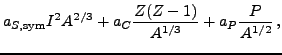To illustrate the fitting and error analysis techniques of the previous section we use them within a simple nuclear mass model. The model expresses nuclear binding energy as a sum of the liquid drop (LD) and shell energies [21]. The LD energy we use closely resembles the Myers-Swiatecki LD formula [22] with symmetry terms in the volume and surface energy parts and a modified Coulomb part. It has the form

$$E_{\rm LD}(N,Z) = a_V A + a_S A^{2/3} + a_{V,\text{sym}} I^2A$$ (23)

$$+ a_{S,\text{sym}}I^2A^{2/3} + a_{C} \frac{Z(Z-1)}{A^{1/3}} + a_P\frac{P}{A^{1/2}}\,,$$

where $I=(N-Z)/A$ and $2P=(-1)^N+(-1)^Z$. The shell energy is modelled by polynomials of $N$ and $Z$:

$$E_{SE}^i(n, z) = x_{i,1} + x_{i,2} n + x_{i,3} z$$

$$+ x_{i,4} n^2 + x_{i,5} nz + x_{i,6} z^2$$

$$+ x_{i,7} n^3 + x_{i,8} n^2z + x_{i,9} nz^2 + x_{i,10} z^3$$

$$+ x_{i,11} n^4 + x_{i,12} n^3z + x_{i,13} n^2z^2$$

$$+ x_{i,14} nz^3 + x_{i,15} z^4\,,$$ (24)

where $z=Z-Z_i$ and $n=N-N_i$. The index $i$ enumerates 15 different rectangular areas on the nuclear mass chart delaminated by magic numbers, see Fig. 1. In each such an area, $N$ and $Z$ values are between given magic numbers $N_i$ and $Z_i$. We restrict parameters of polynomials (24) in such a way that the shell effects be continuous across magic proton and neutron numbers, however, the derivatives thereof can be non-continuous. In this way the model can produce the binding-energy cusps at magic nucleon numbers.

The continuity requirements impose $19$ conditions at semimagic nuclei, see Fig. 1. Each condition results in $p+1$ linear equations for $x_i$, where $p$ is the polynomial order. Thus for the second-, third-, or fourth-order polynomials ($p$=2, 3, or 4) we get $(p+1)\cdot 19$=57, 76, or 85 equations for 90, 150, or 225 parameters, respectively, resulting in 33, 74, or 130 independent variables of the shell energy, Eq. (24). Together with the six parameters of the liquid-drop energy, Eq. (23), the model thus contains 39, 80, or 136 independent parameters.

It should be noted that the model described above is fully linear. This means that the iteration procedure consists of just one step, because matrix $J$ is then constant and the convergence is obtained after just one iteration. In this respect the simple model considered here does not accurately resemble realistic EDF models. However, it allows us to test and showcase all the error analysis methods that can also be used in realistic nonlinear EDF calculations.

Figure 1: (Color online) Areas of nuclear mass chart where the shell energy polynomials of Eq. (24) are defined. The black dots mark lines of semimagic nuclei for which the shell energy polynomials of adjacent rectangles are constrained to have the same values. The numbers in the rectangles show how many nuclei in the given area was used in the fit. Semimagic and magic nuclei belong always to the rectangle to the right and up.

We used the 1995 mass evaluation of Audi and Wapstra [15] as our experimental nuclear binding energies. These masses are outdated, but they serve only for illustrative purposes. The full model with fourth-order polynomials was fitted to $m=2844$ experimental and extrapolated binding energies of nuclei with $A\ge 16$. The resulting set of parameters was used to create metadata masses that approximate the experimental masses with rms deviation of 1.1MeV. In this way, we have constructed the dataset of masses, which is exactly described by the $n=136$ parameters of the full model. Values of the LD parameters used to define the metadata are listed in Table 1.

Table 1: Values and error estimates (in MeV) of the LD parameters. Values defining the metadata are compared with those obtained from fitting the exact model to metadata with a Gaussian noise of 0.1MeV.

Parameter	Defining		Fitted		Error
	value		value		estimate
$a_V$	14.9455		14.9455		0.0008
$a_S$	$-$14.9326		$-$14.9325		0.0024
$a_{V,\text{sym}}$	$-$22.3303		$-$22.3293		0.0053
$a_{S,\text{sym}}$	7.5995		7.5965		0.0068
$a_C$	$-$0.65709		$-$0.65708		0.00005
$a_P$	11.3655		11.3633		0.0187

We do not ascribe any particular physical importance to the model of Eqs. (23) and (24), and we are not really concerned with the question of how well it describes the experimental data, cf. the recent discussion in Refs. [23,24]. The model only serves us for the purpose of creating the metadata, and only these metadata are the subject of the error analysis.

To the metadata given by the fourth-order model we add Gaussian noise of a given standard deviation $\sigma$, i.e., random numbers are added to all of the 2844 metadata masses. We stress here that we do not construct any ensemble of datasets and we do not perform any ensemble averaging. We only have at our disposal the same number of 2844 "experimental" metadata points, for which we know exactly what are the model and noise parameters. From now on, a Gaussian noise of $\sigma=0.1$MeV is used unless explicitly indicated.

The study now concentrates on repeating the least square fits of the above described second-, third-, and fourth-order models to the metadata. The fourth-order model is exact, while the second- and third-order models are inaccurate (see the discussion at the beginning of Sec 2). Note that only the metadata shell effects are imprecisely described by the second- and third-order models--the LD parts of Eq. (23) always have the same form.

Our purpose is to study the fitting procedure, values of parameters, error estimates, and confidence intervals in the situations of exact and inaccurate models. In particular, we analyze dependence of the least square fits on the weights chosen for the definition of the rms deviation. To this end, we chose weights in the form

$$W_j = \frac{mA_j^\alpha}{\sum_{j=1}^m A_j^\alpha},$$ (25)

where $A_j$ is the mass number of the given nuclide and $\alpha$ is a parameter. For $\alpha=0$, one has a 'natural' choice of all weights being equal, $W_j=1$, which is the choice most often used in nuclear mass fits.

However, it is obvious that we can equally well argue in favor of other choices. On the one hand, for $\alpha=-2$, the fit would correspond not to fitting binding energies, but binding energies per particle, $E/A$, which may seem to be a reasonable choice when discussing the LD model parameters. Naturally, this choice simply corresponds to placing more importance in masses of light rather than heavy nuclei. On the other hand, for $\alpha>0$, heavy nuclei are considered to be more important for mass fits than light nuclei, which can be motivated by the fact that these nuclei are closer to the infinite-matter limit. Obviously, these arguments cane be debated, but ultimately one has a freedom of choice in this matter. The parameter $\alpha$ will in the following be varied from $-1$ to 1, and the value of $\alpha=0$ is used whenever not explicitly indicated.

Figure 2: (Color online) The rms deviations of the least square fits (8) as functions of the standard deviation of the Gaussian noise $\sigma$ added to the metadata.

We begin by discussing the influence of the Gaussian noise added to the metadata. In Fig. 2 we show dependence of the rms deviations of the least square fits (8) as functions of the standard deviation of the Gaussian noise $\sigma$. For the exact model, the fitting procedure reproduces the standard deviations of the added noise perfectly well. For the inaccurate models, i.e. for the second- and third-order polynomial fits, one obtains the rms deviations that are higher than the added noise.

Of course, when the added Gaussian noise goes to zero, the rms deviation of the exact model also vanishes. For inaccurate models, in this limiting case the rms deviations level out and converge to about 1.6 and 1.0MeV for the second- and third-order models, respectively. One can say that the inaccurate models introduce their own intrinsic noises, which are not statistical in nature, but represent averaged inaccuracies of the models. One can see that at non-zero Gaussian noise, for inaccurate models the rms deviations are much smaller than the rms of the Gaussian and intrinsic noises. It appears that the intrinsic noise is gradually disappearing inside the Gaussian noise. This is in fact the limit, in which inaccurate models become quite good at describing less well determined experimental data.

In Fig. 3 we show the distributions of fit residuals,

$$\delta e_j = e_j^{\text{exp}} - f_j({\vec x}_0),$$ (26)

obtained by fitting the three considered models to metadata containing the $\sigma=0.1$MeV Gaussian noise. As expected, for the fourth-order (exact) model, the distribution is perfectly Gaussian with the same width of 0.1MeV. For the second- and third-order inaccurate models, the distributions are not only wider, with the widths of 1.6 and 1.0MeV given above, but also do not have exactly Gaussian shapes. This again illustrates the non-statistical nature of the intrinsic noise within inaccurate models.

Figure 3: (Color online) Distributions of fit residuals for three different polynomial fits to metadata. Bin widths are 0.1MeV.

Figure 4: (Color online) Singular values of the fit matrix $J$ of Eq. (10) when three different polynomial orders are used in the least square fit.

Next, we illustrate the problem of eliminating poorly determined model parameters, as explained in Eq. (14). Figure 4 shows the singular values obtained by fitting the second-, third-, and fourth-order models to the metadata. When the third- and fourth-order polynomials are used in the fit, and the maximum numbers of parameters is kept in Eq. (14), a number of parameters become ill defined. This happens because some singular values of matrix $J$ become extremely small. As a result three smallest singular values of the matrix $J$ must be eliminated when the third-order polynomials are used in the fits to the metadata. Similarly, the $14$ smallest singular values have to be eliminated for fourth order polynomials. The extreme smallness of the singular values is a direct result of some redundancy in the model parameters. This is obviously the case in Fig. 1 for those rectangles where the numbers of experimental data are small.

Figure 5: (Color online) The rms deviations (8) of the least square fits to metadata, calculated for the models of Eqs. (23) and (24), as functions of number of singular values kept for matrix $J$, Eq. (14).

As can be seen from Fig. 5, even more unimportant parameters could be eliminated from the fits without losing a significant amount of fit quality. If the second- or third-order polynomials are used to represent the shell effects, only about 60% of the independent uncorrelated model parameters (out of 39 or 80, respectively) are relevant and the remaining 40% do not contribute significantly to the fit, and can be safely removed. For the fourth-order (exact) model this is not the case, and many more parameters (about 85% of 136) are required to go down to the value of the rms deviation equal to 0.1MeV, corresponding to the Gaussian noise in the metadata.

Figure 6: (Color online) Values of the LD parameters obtained from fits with weight factors of Eq. (25), as functions of parameter $\alpha$.

Figures 6 and 7 present results of fits performed for different choices of weights $W_j$, defined in Eq. (25). We first observe that fits of the fourth-order (exact) model give results that are entirely independent of weights. For $\alpha=0$, values of fitted parameters and their error estimates are given in Table 1. Small differences between the fitted values and values defining the metadata, and small values of errors, illustrate the quite small impact of the 0.1MeV Gaussian noise included in the metadata.

The situation is drastically different for fits of the inaccurate models. Here the values of the fitted parameters, shown in Fig. 6, are not only quite different form the exact ones, but also rather strongly depend on the choice of weights. It is clear that the weights strongly affect the balance between the volume and surface parameters. For weights giving greater importance to heavy nuclei ($\alpha>0$), all absolute values of volume and surface parameters decrease. The effect is particularly large for the surface symmetry parameter $a_{S,\text{sym}}$, which for the second-order model decreases from about 9MeV at $\alpha=-1$ to nearly zero at $\alpha=1$.

Figure 7: (Color online) Same as in Fig. 6 but for the error estimates, Eq. (19), of the LD parameters.

Variations of parameters, seen in Fig. 6, are much larger than their error estimates shown in Fig. 7. It means that the standard way of estimating errors, Eq. (19), may give significantly overoptimistic results. We stress here once again that the obtained variations in the LD parameters are induced by imperfect descriptions of shell effects only. One can say that such imperfections do contain smooth particle-number dependencies, which are then captured by the fitting procedure and get transferred to values of the LD parameters.

One can, in principle, argue that macroscopic (LD) and microscopic (shell) effects should not be mixed, but rather should be fitted separately to avoid cross-talk effects described above. This is certainly possible in macroscopic-microscopic models [6] that use separate expressions and/or methods to describe these two features of the mass surface. However, such separation induces ambiguities on its own, see e.g. Ref. [25], and, moreover, it cannot be realized in self-consistent methods, which describe the LD and shell effects by the same set of parameters.

Figure 8: (Color online) Confidence intervals ($99\%$ confidence level) of binding energies of the model defined in Eqs. (23) and (24), calculated in lead isotopes using Eq. (22).

Figure 9: (Color online) Same as in Fig. 8 but for the binding-energy residuals, Eq. (26)

In Figs. 8 and 9 we show the confidence intervals and residuals, Eqs. (22) and (26), respectively, of the binding energies predicted in lead isotopes. For nuclides used in the fit (the range denoted by dotted vertical lines), confidence intervals and residuals obtained for the fourth-order (exact) model nicely reproduce the 0.1MeV Gaussian noise included in the metadata.

The situation is quite different for the inaccurate models, which correspond to fitting the second- or third-order polynomials. In lead isotopes, residuals of the third-order model are still quite small, well below the rms deviation of 1.0MeV, which is the value characterizing this fit. It simply means that for these observables, the model performs quite nicely. However, the confidence intervals tell us that the quality of the model even in lead nuclei is not that great as suggested by small residuals. For the second-order model, residuals become quite high but the confidence intervals indicate that the quality of the model does not, in fact, deteriorate. Confidence intervals and residuals give us diverging evaluations of the quality of the models, because the former represent global characteristics, which depend only on the standard deviations of the parameters, while the latter illustrate only local properties of the models.

An interesting property of the confidence intervals is the fact that, for nuclei outside the fit, the confidence intervals quickly increase, independently of the complexity of the model. This result is in accordance with results obtained within realistic nuclear mass models, whose predictions (for nuclei outside the fit) deviate greatly from each other. On the one hand, such an increase of the confidence intervals is a reflection of poor predictivity of models when they are extrapolated to exotic nuclei. On the other hand, the confidence intervals simply quantify this uncertainty of extrapolation and constitute precise measures of the fact that such extrapolations must be uncertain. This is so because the model parameters are rather loosely defined by the metadata, and therefore, important information is missing from the models.

The discontinuity of confidence intervals at $N=126$ is an artifact of the model, which uses different parameters in rectangles delimited by magic numbers, see Fig. 1. Note that the model ensures the continuity of binding energies, but the confidence intervals need not be continuous.